261. If the nitrogen atom had electronic configuration $$1{s^7}$$ it would have energy lower than that of the normal ground state configuration $$1{s^2}2{s^2}2{p^3}$$ because the electrons would be closer to the nucleus. Yet $$1{s^7}$$ is not observed. It violates
A
Heisenberg’s uncertainty principle
B
Hund’s rule
C
Pauli exclusion principle
D
Bohr postulate of stationary orbits
Answer :
Pauli exclusion principle
262. Few statements are given regarding nodes in the orbitals. Mark the statement which is not correct.
A
In case of $${p_z}$$ - orbital, $$xy$$ plane is a nodal plane.
B
$$ns$$ - orbital has $$\left( {n + 1} \right)$$ nodes.
C
The number of angular nodes is given by $$l.$$
D
The total number of nodes is given by $$\left( {n - 1} \right)$$ i.e. sum of $$l$$ angular nodes and $$\left( {n - l - 1} \right)$$ radial nodes.
Answer :
$$ns$$ - orbital has $$\left( {n + 1} \right)$$ nodes.
263. Uncertainty in position of an electron ( mass of an electron is $$ = 9.1 \times {10^{ - 28}}g$$ ) moving with a velocity of $$3 \times {10^4}cm/s$$ accurate upto $$0.001\% $$ will be ( use $$\frac{h}{{4\pi }}$$ in uncertainty expression where $$h = 6.626 \times {10^{ - 27}}erg\,s$$ )
A
1.93$$\,cm$$
B
3.84$$\,cm$$
C
5.76$$\,cm$$
D
7.68$$\,cm$$
Answer :
1.93$$\,cm$$
264. Which one of the following constitutes a group of the isoelectronic species?
A
$$C_2^{2 - },O_2^ - ,CO,NO$$
B
$$N{O^ + },C_2^{2 - },C{N^ - },{N_2}$$
C
$$C{N^ - },{N_2},O_2^{2 - },C_2^{2 - }$$
D
$${N_2},O_2^ - ,N{O^ + },CO$$
Answer :
$$N{O^ + },C_2^{2 - },C{N^ - },{N_2}$$
265. Two electrons occupying the same orbital are distinguished by
A
Magnetic quantum number
B
Azimuthal quantum number
C
Spin quantum number
D
Principal quantum number
Answer :
Spin quantum number
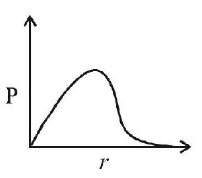
266. $$P$$ is the probability of finding the $$1s$$ electron of hydrogen atom in a spherical shell of infinitesimal thickness, $$dr,$$ at a distance r from the nucleus. The volume of this shell is $${4_\pi }{r^2}dr.$$ The qualitative sketch of the dependence of $$P$$ on $$r$$ is
A
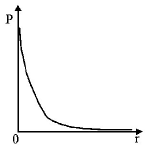

B
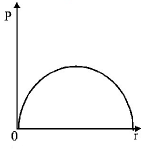

C
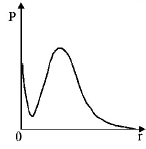

D
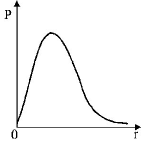

Answer :


267. The dissociation energy of $${H_2}$$ is $$430.53\,kJ\,mo{l^{ - 1}}.$$ If hydrogen is dissociated by illumination with radiation of wavelength $$253.7\,nm$$ the fraction of the radiant energy which will be converted into kinetic energy is given by
A
100%
B
8.82%
C
2.22%
D
1.22%
Answer :
8.82%
268. For a $$d$$-electron, the orbital angular momentum is
A
$$\sqrt 6 \left( {\frac{h}{{2\pi }}} \right)$$
B
$$\sqrt 2 \left( {\frac{h}{{2\pi }}} \right)$$
C
$$\left( {\frac{h}{{2\pi }}} \right)$$
D
$$2\left( {\frac{h}{{2\pi }}} \right)$$
Answer :
$$\sqrt 6 \left( {\frac{h}{{2\pi }}} \right)$$
269. The outermost electronic configuration of the most electronegative element is
A
$$n{s^2}\,n{p^3}$$
B
$$n{s^2}\,n{p^4}$$
C
$$n{s^2}\,n{p^5}$$
D
$$n{s^2}\,n{p^6}$$
Answer :
$$n{s^2}\,n{p^5}$$
270. The energy of a photon is given as $$3.03 \times {10^{ - 19}}J.$$ The wavelength of the photon is
A
6.56$$\,nm$$
B
65.6$$\,nm$$
C
0.656$$\,nm$$
D
656$$\,nm$$
Answer :
656$$\,nm$$