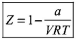101.
A mixture in which the mole ratio of $${H_2}$$ and $${O_2}$$ is 2 : 1 is used to prepare water by the reaction, $$2{H_{2\left( g \right)}} + {O_{2\left( g \right)}} \to 2{H_2}{O_{\left( g \right)}}$$
The total pressure in the container is $$0.8\,atm$$ at $$20{\,^ \circ }C$$ before the reaction. The final pressure at $$120{\,^ \circ }C$$ after reaction is ( assuming $$80\% $$ yield of water )
A
$$1.787\,atm$$
B
$$0.878\,atm$$
C
$$0.787\,atm$$
D
$$1.878\,atm$$
Answer :
$$0.787\,atm$$
102. At high altitudes, water boils at a lower temperature because
A
the atmospheric pressure is high at high altitudes
B
the viscosity of water is reduced at high altitudes
C
the atmospheric pressure is low at high altitudes
D
the surface tension of water is reduced at high altitudes.
Answer :
the atmospheric pressure is low at high altitudes
103. A gas will approach ideal behaviour at
A
low temperature and low pressure.
B
low temperature and high pressure.
C
high temperature and low pressure.
D
high temperature and high pressure.
Answer :
high temperature and low pressure.
104.
For real gases van der Waals equation is written as
$$\left( {P + \frac{{a{n^2}}}{{{V^2}}}} \right)\left( {V - nb} \right) = nRT$$
where $$'a’$$ and $$'b’$$ are van der Waals constants. Two sets of gases are :
$$\eqalign{
& \left( {\text{i}} \right)\,\,{O_2},C{O_2},{H_2}\,{\text{and}}\,He \cr
& \left( {{\text{ii}}} \right)\,\,C{H_4},\,{O_2}\,{\text{and}}\,{H_2} \cr} $$
The gases given in set - I in increasing order of $$'b’$$ and gases given in set - II in decreasing order of $$'a’,$$ are arranged below. Select the correct order from the following :
A
$$\left( {\text{i}} \right)He < {H_2} < C{O_2} < {O_2}$$ $$\left( {{\text{ii}}} \right)C{H_4} > {H_2} > {O_2}$$
B
$$\left( {\text{i}} \right){O_2} < He < {H_2} < C{O_2}$$ $$\left( {{\text{ii}}} \right){H_2} > {O_2} > C{H_4}$$
C
$$\left( {\text{i}} \right)He < {H_2} < {O_2} < C{O_2}$$ $$\left( {{\text{ii}}} \right)C{H_4} > {O_2} > {H_2}$$
D
$$\left( {\text{i}} \right){H_2} < {O_2} < He < C{O_2}$$ $$\left( {{\text{ii}}} \right){O_2} > C{H_4} > {H_2}$$
Answer :
$$\left( {\text{i}} \right)He < {H_2} < {O_2} < C{O_2}$$ $$\left( {{\text{ii}}} \right)C{H_4} > {O_2} > {H_2}$$
105. Copper crystallises in a face centred cubic $$(fcc)$$ lattice with a unit cell length of $$361\,pm.$$ What is the radius of copper atom in $$pm?$$
A
128$$\,pm$$
B
157$$\,pm$$
C
181$$\,pm$$
D
108$$\,pm$$
Answer :
128$$\,pm$$
106. Longest mean free path stands for :
A
$${H_2}$$
B
$${N_2}$$
C
$${O_2}$$
D
$$C{1_2}$$
Answer :
$${H_2}$$
107. If a gas expands at constant temperature, it indicates that
A
kinetic energy of molecules decreases
B
pressure of the gas increases
C
kinetic energy of molecules remains the same
D
number of the molecules of gas increases
Answer :
kinetic energy of molecules remains the same
108. If $$Z$$ is a compressibility factor, van der Waals equation at low pressure can be written as :
A
$$Z = 1 + \frac{{RT}}{{Pb}}$$
B
$$Z = 1 - \frac{a}{{VRT}}$$
C
$$Z = 1 - \frac{{Pb}}{{RT}}$$
D
$$Z = 1 + \frac{{Pb}}{{RT}}$$
Answer :
$$Z = 1 - \frac{a}{{VRT}}$$
109. Kinetic theory of gases proves
A
only Boyle’s law
B
only Charles’ law
C
only Avogadro’s law
D
All of these.
Answer :
All of these.
110. A mixture of dihydrogen and dioxygen at one bar pressure contains $$20\% $$ by weight of dihydrogen. What would be the partial pressure of dihydrogen in bar ?
A
0.8
B
1.8
C
2.8
D
3.0
Answer :
0.8