181. Let $$T_n$$ denote the number of triangles which can be formed using the vertices of a regular polygon of $$n$$ sides. If $${T_{n + 1}} - {T_n} = 21,\,$$ then $$n$$ equals
A
5
B
7
C
6
D
4
Answer :
7
182. The number of ways in which a mixed doubles game in tennis can be arranged from 5 married couples, if no husband and wife play in the same game, is
A
46
B
54
C
60
D
None of these
Answer :
60
183.
The number of ways to fill each of the four cells of the table with a distinct natural number such that the sum of the numbers is 10 and the sums of the numbers placed diagonally are equal, is
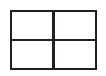
A
$$2!\, \times 2!$$
B
$$4!$$
C
$$2\left( {4!} \right)$$
D
None of these
Answer :
None of these
184. The straight lines $${l_1},{l_2},{l_3}$$ are parallel and lie in the same plane. A total number of $$m$$ points are taken on $${l_1} , n$$ points on $${l_2} , k$$ point on $$l_3 .$$ The maximum number of triangles formed with vertices at these points are :
A
$$^{m + n + k}{C_3}$$
B
$$^{m + n + k}{C_3} - {\,^m}{C_3} - {\,^n}{C_3} - {\,^k}{C_3}$$
C
$$^m{C_3} + {\,^m}{C_3} + {\,^k}{C_3}$$
D
None of these
Answer :
$$^{m + n + k}{C_3} - {\,^m}{C_3} - {\,^n}{C_3} - {\,^k}{C_3}$$
185. The number of numbers divisible by 3 that can be formed by four different even digits is
A
18
B
36
C
0
D
None of these
Answer :
36
186. The sum of all the numbers of four different digits that can be made by using the digits 0, 1, 2 and 3 is
A
26664
B
39996
C
38664
D
None of these
Answer :
38664