81. There are three coplanar parallel lines. If any $$p$$ points are taken on each of the lines, the maximum number of triangles with vertices at these points is
A
$$3{p^2}\left( {p - 1} \right) + 1$$
B
$$3{p^2}\left( {p - 1} \right)$$
C
$${p^2}\left( {4p - 3} \right) $$
D
None of these
Answer :
$${p^2}\left( {4p - 3} \right) $$
82. 5 - digit numbers are to be formed using 2, 3, 5, 7, 9 without repeating the digits. If $$p$$ be the number of such numbers that exceed 20000 and $$q$$ be the number of those that lie between 30000 and 90000, then $$p : q$$ is :
A
$$6 : 5$$
B
$$3 : 2$$
C
$$4 : 3$$
D
$$5 : 3$$
Answer :
$$5 : 3$$
83. From 6 different novels and 3 different dictionaries, 4 novels and 1 dictionary are to be selected and arranged in a row on a shelf so that the dictionary is always in the middle. The number of such arrangements is:
A
less than 500
B
at least 500 but less than 750
C
at least 750 but less than 1000
D
at least 1000
Answer :
at least 1000
84. A shopkeeper sells three varieties of perfumes and he has a large number of bottles of the same size of each variety in his stock. There are 5 places in a row in his showcase. The number of different ways of displaying the three varieties of perfumes in the showcase is
A
6
B
50
C
150
D
None of these
Answer :
150
85.
In the figure, two 4-digit numbers are to be formed by filling the places with digits. The number of different ways in which the places can be filled by digits so that the sum of the numbers formed is also a 4-digit number and in no place the addition is with carrying, is
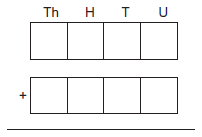
A
$${55^4}$$
B
$$220$$
C
$${45^4}$$
D
None of these
Answer :
None of these
86. The number of ways in which an examiner can assign 30 marks to 8 questions, giving not less than 2 marks to any question, is :
A
$$^{30}{C_7}$$
B
$$^{21}{C_8}$$
C
$$^{21}{C_7}$$
D
$$^{30}{C_8}$$
Answer :
$$^{21}{C_7}$$
87. The number of ways in which the letters of the word ARTICLE can be rearranged so that the even places are always occupied by consonants is
A
$$576$$
B
$$^4{C_3} \times \left( {4!} \right)$$
C
$$2(4!)$$
D
None of these
Answer :
$$576$$
88. The sum of integers from 1 to 100 that are divisible by 2 or 5 is
A
3000
B
3050
C
3600
D
3250
Answer :
3050
89. The number of ways in which 20 different pearls of two colours can be set alternately on a necklace, there being 10 pearls of each colour, is
A
$$9!\, \times 10!$$
B
$$5{\left( {9!} \right)^2}$$
C
$${\left( {9!} \right)^2}$$
D
None of these
Answer :
$$5{\left( {9!} \right)^2}$$
90. The letters of the word $$COCHIN$$ are permuted and all the permutations are arranged in an alphabetical order as in an English dictionary. The number of words that appear before the word $$COCHIN$$ is
A
360
B
192
C
96
D
48
Answer :
96