41.
Four numbers are chosen at random (without replacement) from the set {1, 2, 3, . . . . . 20}.
Statement - 1 : The probability that the chosen numbers when arranged in some order will form an AP is $$\frac{1}{{85}}.$$
Statement - 2 : If the four chosen numbers form an AP, then the set of all possible values of common difference is $$\left( { \pm 1, \pm 2, \pm 3, \pm 4, \pm 5} \right).$$
A
Statement - 1 is true, Statement - 2 is true ; Statement - 2
is not a correct explanation for Statement - 1
B
Statement - 1 is true, Statement - 2 is false
C
Statement - 1 is flase, Statement - 2 is true
D
Statement - 1 is true, Statement - 2 is true ; Statement - 2
is a correct explanation for Statement - 1.
Answer :
Statement - 1 is true, Statement - 2 is false
42. A six faced fair dice is thrown until 1 comes, then the probability that 1 comes in even no. of trials is
A
$$\frac{5}{{11}}$$
B
$$\frac{5}{{6}}$$
C
$$\frac{6}{{11}}$$
D
$$\frac{1}{{6}}$$
Answer :
$$\frac{5}{{11}}$$
43. Let $$0 < P\left( A \right) < 1,\,0 < P\left( B \right) < 1$$ and $$P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( A \right)P\left( B \right),$$ then,
A
$$P\left( {\frac{B}{A}} \right) = P\left( B \right) - P\left( A \right)$$
B
$$P\left( {A' \cup B'} \right) = P\left( {A'} \right) + P\left( {B'} \right)$$
C
$$P\left( {A \cap B} \right) = P\left( {A'} \right)P\left( {B'} \right)$$
D
none of these
Answer :
none of these
44. Given two independent events, if the probability that exactly one of them occurs is $$\frac{{26}}{{49}}$$ and the probability that none of them occurs is $$\frac{{15}}{{49}},$$ then the probability of more probable of the two events is :
A
$$\frac{4}{7}$$
B
$$\frac{6}{7}$$
C
$$\frac{3}{7}$$
D
$$\frac{5}{7}$$
Answer :
$$\frac{4}{7}$$
45. Let $${E^c}$$ denote the complement of an event $$E$$. Let $$E,\,F,\,G$$ be pairwise independent events with $$P\left( G \right) > 0$$ and $$P\left( {E \cap F \cap G} \right) = 0.$$ Then $$P\left( {{E^c} \cap {F^c}|G} \right)$$ equals :
A
$$P\left( {{E^c}} \right) + P\left( {{F^c}} \right)$$
B
$$P\left( {{E^c}} \right) - P\left( {{F^c}} \right)$$
C
$$P\left( {{E^c}} \right) - P\left( F \right)$$
D
$$P\left( E \right) - P\left( {{F^c}} \right)$$
Answer :
$$P\left( {{E^c}} \right) - P\left( F \right)$$
46. Assume that each born child is equally likely to be a boy or a girl. If a family has two children, then the conditional probabilities that both are girls given that $$\left( {\text{i}} \right)$$ the youngest is a girl, $$\left( {{\text{ii}}} \right)$$ at least one is a girl are :
A
$$\frac{1}{2}{\text{ and }}\frac{1}{4}$$
B
$$\frac{1}{3}{\text{ and }}\frac{1}{2}$$
C
$$\frac{1}{3}{\text{ and }}\frac{1}{4}$$
D
$$\frac{1}{2}{\text{ and }}\frac{1}{3}$$
Answer :
$$\frac{1}{2}{\text{ and }}\frac{1}{4}$$
47. There are four machines and it is known that exactly two of them are faulty. They are tested one by one in a random order till both the faulty machines are identified. Then the probability that only two tests will be required is :
A
$$\frac{1}{3}$$
B
$$\frac{1}{6}$$
C
$$\frac{1}{2}$$
D
$$\frac{1}{4}$$
Answer :
$$\frac{1}{6}$$
48. The probability that $$A$$ speaks truth is $$\frac{4}{5}$$ while the probability for $$B$$ is $$\frac{3}{4}.$$ The probability that they contradict each other when asked to speak on a fact is
A
$$\frac{4}{5}$$
B
$$\frac{1}{5}$$
C
$$\frac{7}{20}$$
D
$$\frac{3}{20}$$
Answer :
$$\frac{7}{20}$$
49. A second-order determinant is written down at random using the numbers $$1,\, - 1$$ as elements. The probability that the value of the determinant is nonzero is :
A
$$\frac{1}{2}$$
B
$$\frac{3}{8}$$
C
$$\frac{5}{8}$$
D
$$\frac{1}{3}$$
Answer :
$$\frac{1}{2}$$
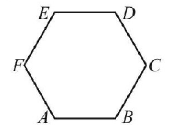
50. Three of the six vertices of a regular hexagon are chosen at random. The probability that the triangle with three vertices is equilateral, equals
A
$$\frac{1}{2}$$
B
$$\frac{1}{5}$$
C
$$\frac{1}{10}$$
D
$$\frac{1}{20}$$
Answer :
$$\frac{1}{10}$$