11.
A body starts from rest on a long inclined plane of slope $${45^ \circ }.$$ The coefficient of friction between the body and the plane varies as $$\mu = 0.3\,x,$$ where $$x$$ is distance travelled down the plane. The body will have maximum speed
(for $$g = 10\,m/{s^2}$$ ) when $$x =$$
A
$$9.8\,m$$
B
$$27\,m$$
C
$$12\,m$$
D
$$3.33\,m$$
Answer :
$$3.33\,m$$
12. A conveyor belt is moving at a constant speed of $$2\,m/s.$$ A box is gently dropped on it. The coefficient of friction between them is $$\mu = 0.5.$$ The distance that the box will move relative to belt before coming to rest on it taking $$g = 10\,m{s^{ - 2}},$$ is
A
$$1.2\,m$$
B
$$0.6\,m$$
C
zero
D
$$0.4\,m$$
Answer :
$$0.4\,m$$
13.
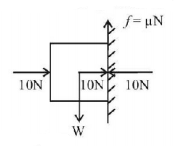
A horizontal force of $$10\,N$$ is necessary to just hold a block stationary against a wall. The coefficient of friction between the block and the wall is $$0.2.$$ The weight of the block is

A
$$20\,N$$
B
$$50\,N$$
C
$$100\,N$$
D
$$2\,N$$
Answer :
$$2\,N$$
14.
A block $$B$$ is pushed momentarily along a horizontal surface with an initial velocity $$V.$$ If $$\mu $$ is the coefficient of sliding friction between $$B$$ and the surface, block $$B$$ will come to rest after a time
A
$$\frac{{g\mu }}{V}$$
B
$$\frac{g}{V}$$
C
$$\frac{V}{g}$$
D
$$\frac{V}{{g\left( \mu \right)}}$$
Answer :
$$\frac{V}{{g\left( \mu \right)}}$$
15. Starting from rest, a body slides down a $${45^ \circ }$$ inclined plane in twice the time it takes to slide down the same distance in the absence of friction. The coefficient of friction between the body and the inclined plane is
A
0.80
B
0.75
C
0.25
D
0.33
Answer :
0.75
16.
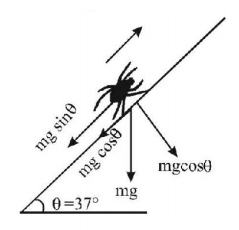
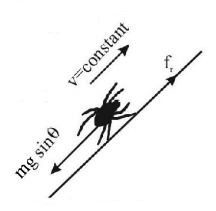
An insect of mass $$m,$$ starts moving on a rough inclined surface from point $$A.$$ As the surface is very sticky, the coefficient of friction between the insect and the incline is $$\mu = 1.$$ Assume that it can move in any direction, up the incline or down the incline then -

A
the maximum possible acceleration of the insect can be $$14\,m/{s^2}$$
B
the maximum possible acceleration of the insect can be $$2\,m/{s^2}$$
C
the insect can move with a constant velocity
D
the insect cannot move with a constant velocity
Answer :
the insect can move with a constant velocity
17. A given object takes $$n$$ times as much time to slide down a $${45^ \circ }$$ rough incline as it takes to slide down a perfectly smooth $${45^ \circ }$$ incline. The coefficient of friction between the object and the incline is
A
$$\left( {1 - \frac{1}{{{n^2}}}} \right)$$
B
$$\frac{1}{{\left( {1 - {n^2}} \right)}}$$
C
$$\sqrt {\left( {1 - \frac{1}{{{n^2}}}} \right)} $$
D
$$\frac{1}{{\sqrt {\left( {1 - {n^2}} \right)} }}$$
Answer :
$$\left( {1 - \frac{1}{{{n^2}}}} \right)$$
18. A block of mass $$m$$ is on an inclined plane of angle $$\theta .$$ The coefficient of friction between the block and the plane is $$\mu $$ and tan $$\theta > \mu .$$ The block is held stationary by applying a force $$P$$ parallel to the plane. The direction of force pointing up the plane is taken to be positive. As $$P$$ is varied from $${P_1} = mg\left( {\sin \theta - \mu \cos \theta } \right)$$ to $${P_2} = mg\left( {\sin \theta + \mu \cos \theta } \right),$$ the frictional force $$f$$ versus $$P$$ graph will look like
A
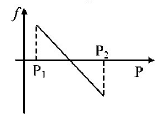

B


C
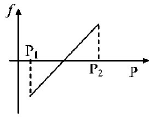
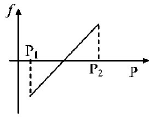
D
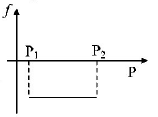

Answer :


19. A smooth block is released at rest on a $${45^ \circ }$$ incline and then slides a distance $$'d'.$$ The time taken to slide is $$'n'$$ times as much to slide on rough incline than on a smooth incline. The coefficient of friction is
A
$${\mu _k} = \sqrt {1 - \frac{1}{{{n^2}}}} $$
B
$${\mu _k} = 1 - \frac{1}{{{n^2}}}$$
C
$${\mu _s} = \sqrt {1 - \frac{1}{{{n^2}}}} $$
D
$${\mu _s} = 1 - \frac{1}{{{n^2}}}$$
Answer :
$${\mu _k} = 1 - \frac{1}{{{n^2}}}$$
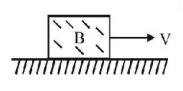
20.
A block of mass $$m$$ is in contact with the cart $$C$$ as shown in the figure.

The coefficient of static friction between the block and the cart is $$\mu .$$ The acceleration $$\alpha $$ of the cart that will prevent the block from falling satisfies
A
$$\alpha > \frac{{mg}}{\mu }$$
B
$$\alpha > \frac{g}{{\mu m}}$$
C
$$\alpha \geqslant \frac{g}{\mu }$$
D
$$\alpha < \frac{g}{\mu }$$
Answer :
$$\alpha \geqslant \frac{g}{\mu }$$