31. What will be the maximum speed of a car on a road turn of radius $$30\,m,$$ if the coefficient of friction between the tyres and the road is 0.4? (Take $$g = 9.8\,m/{s^2}$$ )
A
$$10.84\,m/s$$
B
$$9.84\,m/s$$
C
$$8.84\,m/s$$
D
$$6.84\,m/s$$
Answer :
$$10.84\,m/s$$
32.
A block is placed on a rough horizontal plane.A time dependent horizontal force $$F = kt$$ acts on the block, where $$k$$ is a positive constant. The acceleration - time graph of the block is :
A


B


C
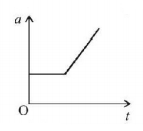

D


Answer :


33.
If $$\mu $$ be the coefficient of friction between the block and the cart, horizontal acceleration of the cart that is required to prevent block $$B$$ from falling is:
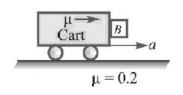
A
$$\frac{\mu }{g}$$
B
$$\frac{g}{\mu }$$
C
$$g$$
D
$$\left( {{\mu ^2} + 1} \right)g$$
Answer :
$$\frac{g}{\mu }$$
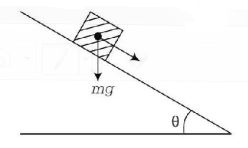
34. A block of base $$10cm \times 10cm$$ and height $$15cm$$ is kept on an inclined plane. The coefficient of friction between them is $$\sqrt 3 .$$ The inclination $$\theta $$ of this inclined plane from the horizontal plane is gradually increased from $${0^ \circ }.$$ Then
A
at $$\theta = 30°,$$ the block will start sliding down the plane
B
the block will remain at rest on the plane up to certain $$\theta $$ and then it will topple
C
at $$\theta = 60°,$$ the block will start sliding down the plane and continue to do so at higher angles
D
at $$\theta = 60°,$$ the block will start sliding down the plane and on further increasing $$\theta ,$$ it will topple at certain $$\theta .$$
Answer :
the block will remain at rest on the plane up to certain $$\theta $$ and then it will topple
35.
A plank with a box on it at one end is gradually raised about the other end. As the angle of inclination with the horizontal reaches $${30^ \circ },$$ the box starts to slip and slides $$4.0\,m$$ down the plank in $$4.0\,s.$$ The coefficients of static and kinetic friction between the box and the plank will be, respectively

A
0.6 and 0.6
B
0.6 and 0.5
C
0.5 and 0.6
D
0.4 and 0.3
Answer :
0.6 and 0.5
36.
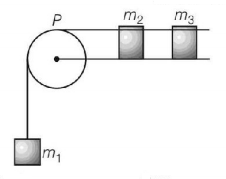
A system consists of three masses $${m_1},{m_2}$$ and $${m_3}$$ connected by a string passing over a pulley $$P.$$ The mass $${m_1}$$ hangs freely and $${m_2}$$ and $${m_3}$$ are on a rough horizontal table (the coefficient of friction = $$\mu $$ ). The pulley is frictionless and of negligible mass. The downward acceleration of mass $${m_1}$$ is (Assume, $${m_1} = {m_2} = {m_3} = m$$ )
A
$$\frac{{g\left( {1 - g\mu } \right)}}{9}$$
B
$$\frac{{2g\mu }}{3}$$
C
$$\frac{{g\left( {1 - 2\mu } \right)}}{3}$$
D
$$\frac{{g\left( {1 - 2\mu } \right)}}{2}$$
Answer :
$$\frac{{g\left( {1 - 2\mu } \right)}}{3}$$
37.
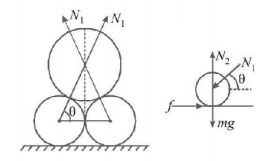
Two identical smooth surfaced solid cylinders of radius $$r$$ are placed touching along their lengths on a horizontal surface. A third cylinder of same material but twice the radius of that of the cylinders is placed lengthwise on them so that the system remains at rest. If all three cylinders have the same length, then minimum value of the coefficient of friction between smaller cylinders and the surface is:

A
$$\frac{1}{{\sqrt 2 }}$$
B
$$\frac{1}{3}$$
C
$$\frac{1}{{3\sqrt 2 }}$$
D
None of these
Answer :
$$\frac{1}{{3\sqrt 2 }}$$
38. It is difficult to move a cycle with brakes on because
A
rolling friction opposes motion on road
B
sliding friction opposes motion on road
C
rolling friction is more than sliding friction
D
sliding friction is more than rolling friction
Answer :
sliding friction is more than rolling friction
39. A car is negotiating a curved road of radius $$R.$$ The road is banked at angle $$\theta .$$ The coefficient of friction between the tyres of the car and the road is $${\mu _s}.$$ The maximum safe velocity on this road is
A
$$\sqrt {gR\left( {\frac{{{\mu _s} + \tan \theta }}{{1 - {\mu _s}\tan \theta }}} \right)} $$
B
$$\sqrt {\frac{g}{R}\left( {\frac{{{\mu _s} + \tan \theta }}{{1 - {\mu _s}\tan \theta }}} \right)} $$
C
$$\sqrt {\frac{g}{{{R^2}}}\left( {\frac{{{\mu _s} + \tan \theta }}{{1 - {\mu _s}\tan \theta }}} \right)} $$
D
$$\sqrt {g{R^2}\left( {\frac{{{\mu _s} + \tan \theta }}{{1 - {\mu _s}\tan \theta }}} \right)} $$
Answer :
$$\sqrt {gR\left( {\frac{{{\mu _s} + \tan \theta }}{{1 - {\mu _s}\tan \theta }}} \right)} $$