151. A man throws balls with the same speed vertically upwards one after the other at an interval of $$2\,s.$$ What should be the speed of the throw so that more than two balls are in the sky at any time? (Take $$g = 9.8\,m/{s^2}$$ )
A
Any speed less than $$19.6\,m/s$$
B
Only with speed $$19.6\,m/s$$
C
More than $$19.6\,m/s$$
D
At least $$9.8\,m/s$$
Answer :
More than $$19.6\,m/s$$
152. A bus starts moving with acceleration $$2\,m/{s^2}.$$ A cyclist $$96\,m$$ behind the bus starts simultaneously towards the bus at $$20\,m/s.$$ After what time will he be able to overtake the bus?
A
$$4\,\sec $$
B
$$8\,\sec $$
C
$$18\,\sec $$
D
$$16\,\sec $$
Answer :
$$8\,\sec $$
153. If $$\left| {A \times B} \right| = \sqrt 3 A \cdot B,$$ then the value of $$\left| {A + B} \right|$$ is
A
$${\left( {{A^2} + {B^2} + AB} \right)^{\frac{1}{2}}}$$
B
$${\left( {{A^2} + {B^2} + \frac{{AB}}{{\sqrt 3 }}} \right)^{\frac{1}{2}}}$$
C
$$A + B$$
D
$${\left( {{A^2} + {B^2} + \sqrt 3 AB} \right)^{\frac{1}{2}}}$$
Answer :
$${\left( {{A^2} + {B^2} + AB} \right)^{\frac{1}{2}}}$$
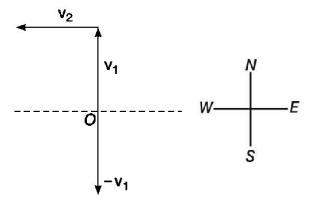
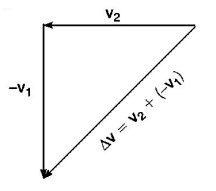
154. A bus is moving on a straight road towards North with a uniform speed of $$50\,km/h.$$ If the speed remains unchanged after turning through $${90^ \circ },$$ the increase in the velocity of bus in the turning process is
A
$$70.7\,km/h$$ along South-West direction
B
zero
C
$$50\,km/h$$ along West
D
$$70.7\,km/h$$ along North-West direction
Answer :
$$70.7\,km/h$$ along South-West direction
155. The displacement $$x$$ of a particle at the instant when its velocity is $$v$$ is given by $$v = \sqrt {3x + 16} .$$ Its acceleration and initial velocity are
A
1.5 units, 4 units
B
3 units, 4 units
C
16 units, 1.6 units
D
16 units, 3 units
Answer :
1.5 units, 4 units
156. A plane flying horizontally at a height of $$1500\,m$$ with a velocity of $$200\,m{s^{ - 1}}$$ passes directly overhead on antiaircraft gun. Then the angle with the horizontal at which the gun should be fired from the shell with a muzzle velocity of $$400\,m{s^{ - 1}}$$ to hit the plane, is
A
$${90^ \circ }$$
B
$${60^ \circ }$$
C
$${30^ \circ }$$
D
$${45^ \circ }$$
Answer :
$${60^ \circ }$$
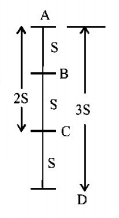
157. Let $$A,B,C,D$$ be points on a vertical line such that $$AB = BC = CD.$$ If a body is released from position $$A,$$ the times of descent through $$AB,BC$$ and $$CD$$ are in the ratio.
A
$$1:\sqrt 3 - \sqrt 2 :\sqrt 3 + \sqrt 2 $$
B
$$1:\sqrt 2 - 1:\sqrt 3 - \sqrt 2 $$
C
$$1:\sqrt 2 - 1:\sqrt 3 $$
D
$$1:\sqrt 2 :\sqrt 3 - 1$$
Answer :
$$1:\sqrt 2 - 1:\sqrt 3 - \sqrt 2 $$
158. The position $$x$$ of a particle varies with time $$t,$$ as $$x = a{t^2} - b{t^3}.$$ The acceleration of the particle will be zero at time $$t$$ equals to
A
zero
B
$$\frac{a}{{3b}}$$
C
$$\frac{{2a}}{{3b}}$$
D
$$\frac{a}{b}$$
Answer :
$$\frac{a}{{3b}}$$
159. A particle crossing the origin of co-ordinates at time $$t = 0,$$ moves in the $$xy$$ -plane with a constant acceleration a in the $$y$$-direction. If its equation of motion is $$y = b{x^2}$$ ($$b$$ is a constant), its velocity component in the $$x$$-direction is
A
$$\sqrt {\frac{{2b}}{a}} $$
B
$$\sqrt {\frac{a}{{2b}}} $$
C
$$\sqrt {\frac{a}{b}} $$
D
$$\sqrt {\frac{b}{a}} $$
Answer :
$$\sqrt {\frac{a}{{2b}}} $$
160. If $$\left| {\vec A \times \vec B} \right| = \sqrt 3 \vec A.\vec B,$$ then the value of $$\left| {\vec A + \vec B} \right|$$ is:
A
$${\left( {{A^2} + {B^2} + \frac{{AB}}{{\sqrt 3 }}} \right)^{\frac{1}{2}}}$$
B
$$A + B$$
C
$${\left( {{A^2} + {B^2} + \sqrt 3 AB} \right)^{\frac{1}{2}}}$$
D
$${\left( {{A^2} + {B^2} + AB} \right)^{\frac{1}{2}}}$$
Answer :
$${\left( {{A^2} + {B^2} + AB} \right)^{\frac{1}{2}}}$$