51.
Two blocks $$A$$ and $$B$$ of masses $$3m$$ and $$m$$ respectively are connected by a massless and inextensible string. The whole system is suspended by a massless spring as shown in figure. The magnitudes of acceleration of $$A$$ and $$B$$ immediately after the string is cut, are respectively

A
$$g,\frac{g}{3}$$
B
$$\frac{g}{3},g$$
C
$$g,g$$
D
$$\frac{g}{3},\frac{g}{3}$$
Answer :
$$\frac{g}{3},g$$
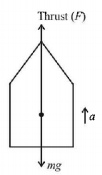
52. A rocket with a lift-off mass $$3.5 \times {10^4}\,kg$$ is blasted upwards with an initial acceleration of $$10m/{s^2}.$$ Then the initial thrust of the blast is
A
$$3.5 \times {10^5}\,N$$
B
$$7.0 \times {10^5}\,N$$
C
$$14.0 \times {10^5}\,N$$
D
$$1.75 \times {10^5}\,N$$
Answer :
$$7.0 \times {10^5}\,N$$
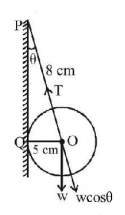
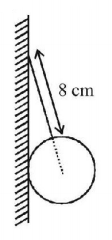
53.
A uniform sphere of weight $$W$$ and radius $$5\,cm$$ is being held by a string as shown in the figure. The tension in the string will be :
A
$$12\frac{W}{5}$$
B
$$5\frac{W}{{12}}$$
C
$$13\frac{W}{5}$$
D
$$13\frac{W}{{12}}$$
Answer :
$$13\frac{W}{{12}}$$
54. Five persons $$A,B,C,D$$ and $$E$$ are pulling a cart of mass $$100\,kg$$ on a smooth surface and cart is moving with acceleration $$3\,m/{s^2}$$ in east direction. When person $$A$$ stops pulling, it moves with acceleration $$1\,m/{s^2}$$ in the west direction. When person $$B$$ stops pulling, it moves with acceleration $$24\,m/{s^2}$$ in the north direction. The magnitude of acceleration of the cart when only $$A$$ and $$B$$ pull the cart keeping their directions same as the old directions, is
A
$$26\,m/{s^2}$$
B
$$3\sqrt {71} \,m/{s^2}$$
C
$$30\,m/{s^2}$$
D
$$25\,m/{s^2}$$
Answer :
$$25\,m/{s^2}$$
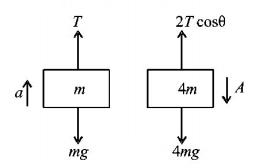
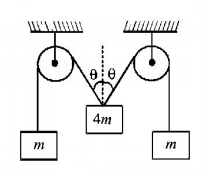
55.
In the figure shown, the pulleys and strings are massless. The acceleration of the block of mass $$4m$$ just after the system is released from rest is
$$\left( {\theta = {{\sin }^{ - 1}}\frac{3}{5}} \right)$$
A
$$\frac{{2g}}{5}\,{\text{downwards}}$$
B
$$\frac{{2g}}{5}\,{\text{upwards}}$$
C
$$\frac{{5g}}{{11}}\,{\text{downwards}}$$
D
$$\frac{{5g}}{{11}}\,{\text{upwards}}$$
Answer :
$$\frac{{5g}}{{11}}\,{\text{downwards}}$$
56. A particle of mass $$0.3kg$$ subject to a force $$F = - kx$$ with $$k = 15 N/m.$$ What will be its initial acceleration if it is released from a point $$20cm$$ away from the origin ?
A
$$15m/{s^2}$$
B
$$3m/{s^2}$$
C
$$10m/{s^2}$$
D
$$5m/{s^2}$$
Answer :
$$10m/{s^2}$$
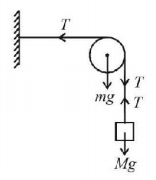
57.
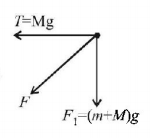
A string of negligible mass going over a clamped pulley of mass $$m$$ supports a block of mass $$M$$ as shown in the figure. The force on the pulley by the clamp is given by

A
$$\sqrt 2 Mg$$
B
$$\sqrt 2 \,mg$$
C
$$\sqrt {{{\left( {M + m} \right)}^2} + {m^2}} g$$
D
$$\sqrt {{{\left( {M + m} \right)}^2} + {M^2}} g$$
Answer :
$$\sqrt {{{\left( {M + m} \right)}^2} + {M^2}} g$$
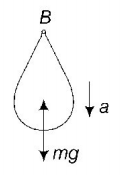
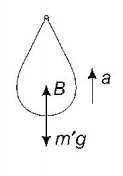
58. A balloon with mass $$m$$ is descending down with an acceleration $$a$$ (where, $$a < g$$ ). How much mass should be removed from it so that it starts moving up with an acceleration $$a$$ ?
A
$$\frac{{2ma}}{{g + a}}$$
B
$$\frac{{2ma}}{{g - a}}$$
C
$$\frac{{ma}}{{g + a}}$$
D
$$\frac{{ma}}{{g - a}}$$
Answer :
$$\frac{{2ma}}{{g + a}}$$
59. A spring balance is attached to the ceiling of a lift. A man hangs his bag on the spring and the spring reads $$49N,$$ when the lift is stationary. If the lift moves downward with an acceleration of $$5m/{s^2},$$ the reading of the spring balance will be
A
$$24\,N$$
B
$$74\,N$$
C
$$15\,N$$
D
$$49\,N$$
Answer :
$$24\,N$$
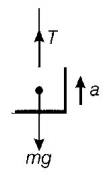
60. A lift of mass $$1000\,kg$$ is moving upwards with an acceleration of $$1\,m/{s^2}.$$ The tension developed in the string, which is connected to lift is $$\left( {g = 9.8\,m/{s^2}} \right)$$
A
$$9800\,N$$
B
$$10800\,N$$
C
$$11000\,N$$
D
$$10000\,N$$
Answer :
$$10800\,N$$