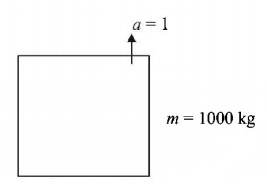
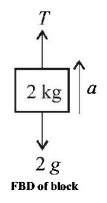
61. A person of mass $$60\,kg$$ is inside a lift of mass $$940\,kg$$ and presses the button on control panel. The lift starts moving upwards with an acceleration $$1.0\,m/s.$$ If $$g = 10\,m{s^{ - 2}},$$ the tension in the supporting cable is
A
$$8600\,N$$
B
$$9680\,N$$
C
$$11000\,N$$
D
$$1200\,N$$
Answer :
$$11000\,N$$
62.
A weight $$W$$ is supported by two cables as shown. The tension in the cable making angle $$\theta $$ with horizontal will be the minimum when the value of $$\theta $$ is
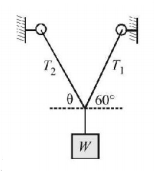
A
0
B
$${30^ \circ }$$
C
$${60^ \circ }$$
D
$${45^ \circ }$$
Answer :
$${30^ \circ }$$
63.
Three blocks $$A, B$$ and $$C$$ of masses $$4\,kg, 2\,kg$$ and $$1\,kg$$ respectively, are in contact on a frictionless surface, as shown. If a force of $$14\,N$$ is applied on the $$4\,kg$$ block, then the contact force between $$A$$ and $$B$$ is

A
$$2\,N$$
B
$$6\,N$$
C
$$8\,N$$
D
$$18\,N$$
Answer :
$$6\,N$$
64.
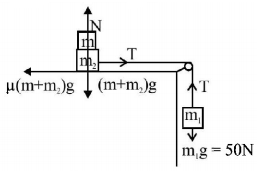
Two masses $${m_1} = 5 kg$$ and $${m_2} = 10 kg,$$ connected by an inextensible string over a frictionless pulley, are moving as shown in the figure. The coefficient of friction of horizontal surface is 0.15. The minimum weight $$m$$ that should be put on top of $${m_2}$$ to stop the motion is:
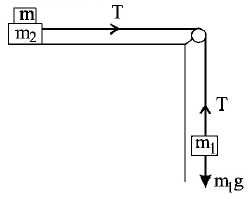
A
$$18.3 kg$$
B
$$27.3 kg$$
C
$$43.3 kg$$
D
$$10.3 kg$$
Answer :
$$27.3 kg$$
65.
A mass of $$1\,kg$$ is suspended by a thread. It is
(i) lifted up with an acceleration $$4.9\,m/{s^2},$$
(ii) lowered with an acceleration $$4.9\,m/{s^2}.$$
The ratio of the tensions is
A
$$3:1$$
B
$$1:2$$
C
$$1:3$$
D
$$2:1$$
Answer :
$$3:1$$
66.
For the system shown in figure, the correct expression is
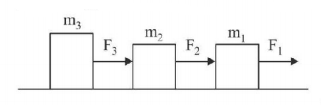
A
$${F_3} = {F_1} + {F_2}$$
B
$${F_3} = \frac{{{m_3}F}}{{{F_1} + {F_2} + {F_3}}}$$
C
$${F_3} = \frac{{{m_3}F}}{{{m_1} + {m_2} + {m_3}}}$$
D
$${F_3} = \frac{{{m_3}F}}{{{m_1} + {m_2}}}$$
Answer :
$${F_3} = \frac{{{m_3}F}}{{{m_1} + {m_2} + {m_3}}}$$
67. A ball of mass $$0.2\,kg$$ is thrown vertically upwards by applying a force by hand. If the hand moves $$0.2\,m$$ while applying the force and the ball goes upto $$2\,m$$ height further, find the magnitude of the force. (Consider $$g = 10\,m/{s^2}$$ ).
A
$$4\,N$$
B
$$16\,N$$
C
$$20\,N$$
D
$$22\,N$$
Answer :
$$22\,N$$
68.
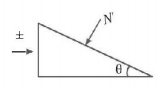
In the diagram shown, friction is completely absent. If a force $$F$$ has been applied on the wedge such that it moves with a constant velocity than value of normal reaction $$N'$$ is
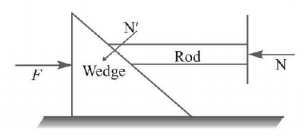
A
$$ > F$$
B
$$ < F$$
C
$$ = F$$
D
cannot find
Answer :
$$ > F$$
69.
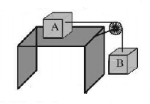
A block $$A$$ of mass $$7\,kg$$ is placed on a frictionless table. A thread tied to it passes over a frictionless pulley and carries a body $$B$$ of mass $$3\,kg$$ at the other end. The acceleration of the system is (given $$g = 10\;m{s^{ - 2}}$$ )
A
$$100\,m{s^{ - 2}}$$
B
$$3\,m{s^{ - 2}}$$
C
$$10\,m{s^{ - 2}}$$
D
$$30\,m{s^{ - 2}}$$
Answer :
$$3\,m{s^{ - 2}}$$
70.
Two blocks of masses $$2\,kg$$ and $$4\,kg$$ are attached by an inextensible light string as shown in the figure. If a force of $$120\,N$$ pulls the blocks vertically upward, the tension in the string is
(take $$g = 10\,m{s^{ - 2}}$$ )

A
$$20\,N$$
B
$$15\,N$$
C
$$35\,N$$
D
$$40\,N$$
Answer :
$$40\,N$$