71. A $$10\,N$$ force is applied on a body produces an acceleration of $$1\,m/{s^2}.$$ The mass of the body is
A
$$5\,kg$$
B
$$10\,kg$$
C
$$15\,kg$$
D
$$20\,kg$$
Answer :
$$10\,kg$$
72.
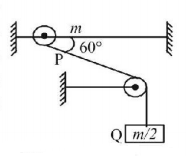
A smooth ring $$P$$ of mass $$m$$ can slide on a fixed horizontal rod. A string tied to the ring passes over a fixed pulley and carries a block $$Q$$ of mass $$\left( {\frac{m}{2}} \right)$$ as shown in the figure.
At an instant, the string between the ring and the pulley makes an angle $${60^ \circ }$$ with the rod. The initial acceleration of the ring is
A
$$\frac{{2g}}{3}$$
B
$$\frac{{2g}}{6}$$
C
$$\frac{{2g}}{9}$$
D
$$\frac{{g}}{3}$$
Answer :
$$\frac{{2g}}{9}$$
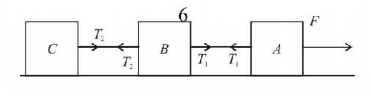
73.
Three identical blocks of masses $$m = 2\,kg$$ are drawn by a force $$F = 10.2\,N$$ with an acceleration of $$0.6\,m{s^{ - 2}}$$ on a frictionless surface, then what is the tension (in $$N$$) in the string between the blocks $$B$$ and $$C$$ ?

A
9.2
B
3.4
C
4
D
9.8
Answer :
3.4
74.
One end of a massless rope, which passes over a massless and frictionless pulley $$P$$ is tied to a hook $$C$$ while the other end is free. Maximum tension that the rope can bear is $$360N.$$ With what value of maximum safe acceleration (in $$m{s^{ - 2}}$$ ) can a man of $$60kg$$ climb on the rope?

A
16
B
6
C
4
D
8
Answer :
4
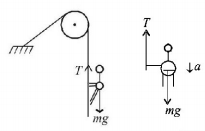
75.
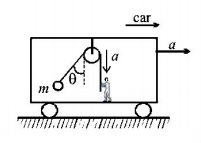
A bob is hanging over a pulley inside a car through a string. The second end of the string is in the hand of a person standing in the car. The car is moving with constant acceleration $$a$$ directed horizontally as shown in figure. Other end of the string is pulled with constant acceleration $$a$$ vertically. The tension in the string is equal to
A
$$m\sqrt {{g^2} + {a^2}} $$
B
$$m\sqrt {{g^2} + {a^2}} - ma$$
C
$$m\sqrt {{g^2} + {a^2}} + ma$$
D
$$m\left( {g + a} \right)$$
Answer :
$$m\sqrt {{g^2} + {a^2}} + ma$$
76. A lift is moving down with acceleration $$a.$$ A man in the lift drops a ball inside the lift. The acceleration of the ball as observed by the man in the lift and a man standing stationary on the ground are respectively
A
$$g,g$$
B
$$g - a,g - a$$
C
$$g - a,g$$
D
$$a,g$$
Answer :
$$g - a,g$$
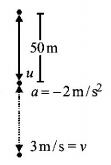
77. A parachutist after bailing out falls $$50m$$ without friction. When parachute opens, it decelerates at $$2m/{s^2}.$$ He reaches the ground with a speed of $$3m/s.$$ At what height, did he bail out ?
A
$$182m$$
B
$$91m$$
C
$$111m$$
D
$$293m$$
Answer :
$$293m$$
78. A person of mass $$60\,kg$$ is inside a lift of mass $$940\,kg$$ and presses the button on control panel. The lift starts moving upwards with an acceleration $$1.0\,m/{s^2}.$$ If $$g = 10\,m/{s^2},$$ the tension in the supporting cable is
A
$$9680\,N$$
B
$$11000\,N$$
C
$$1200\,N$$
D
$$8600\,N$$
Answer :
$$11000\,N$$
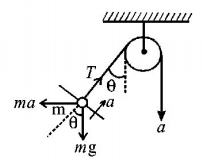
79. A block of mass $$m$$ is placed on a smooth wedge of inclination $$\theta .$$ The whole system is accelerated horizontally, so that the block does not slip on the wedge. The force exerted by the wedge on the block ($$g$$ is acceleration due to gravity) will be
A
$$mg\cos \theta $$
B
$$mg\sin \theta $$
C
$$mg$$
D
$$\frac{{mg\sin \theta }}{{\cos \theta }}$$
Answer :
$$\frac{{mg\sin \theta }}{{\cos \theta }}$$
80.
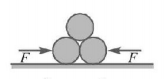
Two smooth cylindrical bars weighing $$W$$ each lie next to each other in contact. A similar third bar is placed over the two bars as shown in figure. Neglecting friction, the minimum horizontal force on each lower bar necessary to keep them together is
A
$$\frac{W}{2}$$
B
$$W$$
C
$$\frac{W}{{\sqrt 3 }}$$
D
$$\frac{W}{{2\sqrt 3 }}$$
Answer :
$$\frac{W}{{2\sqrt 3 }}$$