81.
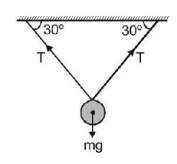
A solid sphere of $$2\,kg$$ is suspended from a horizontal beam by two supporting wires as shown in fig. Tension in each wire is approximately
$$\left( {g = 10\,m{s^{ - 2}}} \right)$$
A
$$30\,N$$
B
$$20\,N$$
C
$$10\,N$$
D
$$5\,N$$
Answer :
$$20\,N$$
82.
A monkey of mass $$20\,kg$$ is holding a vertical rope. The rope will not break when a mass of $$25\,kg$$ is suspended from it but will break if the mass exceeds $$25\,kg.$$ What is the maximum acceleration with which the monkey can climb up along the rope ?
$$\left( {g = 10\,m/{s^2}} \right)$$
A
$$2.5\,m/s$$
B
$$5\,m/{s^2}$$
C
$$10\,m/{s^2}$$
D
$$25\,m/{s^2}$$
Answer :
$$2.5\,m/s$$
83. A player caught a cricket ball of mass $$150g$$ moving at a rate of $$20m/s.$$ If the catching process is completed in $$0.1s,$$ the force of the blow exerted by the ball on the hand of the player is equal to
A
$$150N$$
B
$$3N$$
C
$$30N$$
D
$$300N$$
Answer :
$$30N$$
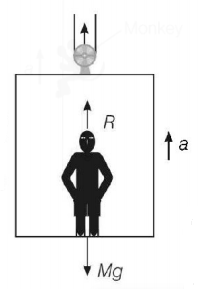
84. A man weighs $$80\,kg.$$ He stands on a weighing scale in a lift which is moving upwards with a uniform acceleration of $$5\,m/{s^2}.$$ What would be the reading on the scale? (Take $$g = 10\,\,m/{s^2}$$ )
A
$$800\,N$$
B
$$1200\,N$$
C
Zero
D
$$400\,N$$
Answer :
$$1200\,N$$
85.
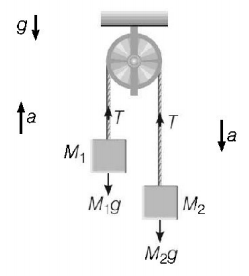
Two masses $${M_1} = 5{\text{ }}kg,{M_2} = 10{\text{ }}kg$$ are connected at the ends of an inextensible string passing over a frictionless pulley as shown. When masses are released, then acceleration of masses will be

A
$$g$$
B
$$\frac{g}{2}$$
C
$$\frac{g}{3}$$
D
$$\frac{g}{4}$$
Answer :
$$\frac{g}{3}$$
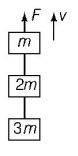
86.
Three blocks with masses $$m,\,2m$$ and $$3m$$ are connected by strings, as shown in the figure. After an upward force $$F$$ is applied on block $$m,$$ the masses move upward at constant speed $$v.$$ What is the net force on the block of mass $$2m$$ ? ($$g$$ is the acceleration due to gravity).
A
Zero
B
$$2\,mg$$
C
$$3\,mg$$
D
$$6\,mg$$
Answer :
Zero
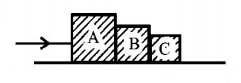
87.
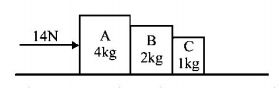
Three blocks $$A,B$$ and $$C$$ of masses $$4\,kg,2\,kg$$ and $$1\,kg$$ respectively, are in contact on a frictionless surface, as shown. If a force of $$14\,N$$ is applied on the $$4\,kg$$ block then the contact force between $$A$$ and $$B$$ is
A
$$6\,N$$
B
$$8\,N$$
C
$$18\,N$$
D
$$2\,N$$
Answer :
$$6\,N$$
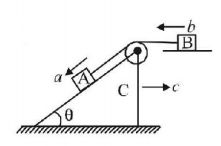
88.
In the figure acceleration of bodies $$A,B$$ and $$C$$ are shown with directions. Values $$b$$ and $$c$$ are w.r.t. ground whereas $$a$$ is acceleration of block $$A$$ w.r.t. wedge $$C.$$
Acceleration of block $$A$$ w.r.t ground is
A
$$\sqrt {{{\left( {b + c} \right)}^2} + {a^2}} $$
B
$$c - \left( {a + b} \right)\cos \theta $$
C
$$\sqrt {{{\left( {b + c} \right)}^2} + {c^2} - 2\left( {b + c} \right).c.\cos \theta } $$
D
$$\sqrt {{{\left( {b + c} \right)}^2} + {c^2} + 2\left( {b + c} \right).c.\cos \theta } $$
Answer :
$$\sqrt {{{\left( {b + c} \right)}^2} + {c^2} - 2\left( {b + c} \right).c.\cos \theta } $$
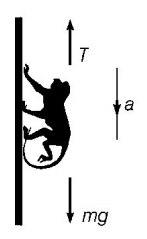
89. A monkey is descending from the branch of a tree with constant acceleration. If the breaking strength is 75% of the weight of the monkey, the minimum acceleration with which monkey can slide down without breaking the branch is
A
$$g$$
B
$$\frac{{3g}}{4}$$
C
$$\frac{g}{4}$$
D
$$\frac{g}{2}$$
Answer :
$$\frac{g}{4}$$
90. An overweight acrobat, "weighing" in at $$115\,kg,$$ wants to perform a single hand stand. He tries to cheat by resting one foot against a smooth frictionless vertical wall. The horizontal force there is $$130\,N.$$ What is the magnitude of the force exerted by the floor on his hand? Answer in $$N.$$
A
1134
B
1257
C
997
D
1119
Answer :
1134