41.
A toy car rolls down the inclined plane as shown in the fig. It loops at the bottom. What is the relation between $$H$$ and $$h$$?

A
$$\frac{H}{h} = 2$$
B
$$\frac{H}{h} = 3$$
C
$$\frac{H}{h} = 4$$
D
$$\frac{H}{h} = 5$$
Answer :
$$\frac{H}{h} = 5$$
42. A solid homogeneous sphere of mass $$M$$ and radius $$R$$ is moving on a rough horizontal surface, partly rolling and partly sliding. During this kind of motion of the sphere
A
total kinetic energy is conserved
B
the angular momentum of the sphere about the point of contact with the plane is conserved
C
only the rotational kinetic energy about the centre of mass is conserved
D
angular momentum about the centre of mass is conserved
Answer :
the angular momentum of the sphere about the point of contact with the plane is conserved
43.
Four particles of masses $${m_1},{m_2},{m_3}$$ and $${m_4}$$ are placed at the vertices $$A,B,C$$ and $$D$$ as respectively of a square shown. The $$COM$$ of the system will lie at diagonal $$AC$$ if
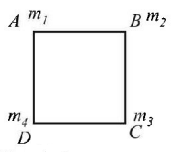
A
$${m_1} = {m_3}$$
B
$${m_2} = {m_4}$$
C
$${m_1} = {m_2}$$
D
$${m_3} = {m_4}$$
Answer :
$${m_2} = {m_4}$$
44.
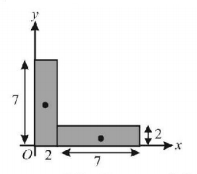
A metal sheet $$14\,cm \times 2\,cm$$ of uniform thickness is cut into two pieces of width $$2\,cm.$$ The two pieces are joined and laid along $$XY$$ plane as shown. The centre of mass has the coordinates
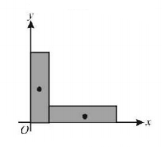
A
$$\left( {1,1} \right)$$
B
$$\left( {\frac{7}{2},\frac{7}{2}} \right)$$
C
$$\left( {\frac{{13}}{4},\frac{9}{4}} \right)$$
D
$$\left( {\frac{{12}}{7},\frac{8}{7}} \right)$$
Answer :
$$\left( {\frac{{13}}{4},\frac{9}{4}} \right)$$
45. A thin horizontal circular disc is rotating about a vertical axis passing through its centre. An insect is at rest at a point near the rim of the disc. The insect now moves along a diameter of the disc to reach its other end. During the journey of the insect, the angular speed of the disc.
A
continuously decreases
B
continuously increases
C
first increases and then decreases
D
remains unchanged
Answer :
first increases and then decreases
46.
A wheel of bicycle is rolling without slipping on a level road. The velocity of the centre of mass is $${v_{CM}},$$ then true statement is
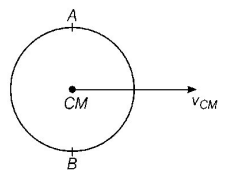
A
The velocity of point $$A$$ is $$2{v_{CM}}$$ and velocity of point $$B$$ is zero
B
The velocity of point $$A$$ is zero and velocity of point $$B$$ is $$2{v_{CM}}$$
C
The velocity of point $$A$$ is $$2{v_{CM}}$$ and velocity of point $$B$$ is $$ - {v_{CM}}$$
D
The velocities of both $$A$$ and $$B$$ are $${v_{CM}}$$
Answer :
The velocity of point $$A$$ is $$2{v_{CM}}$$ and velocity of point $$B$$ is zero
47. Two bodies have their moments of inertia $$I$$ and $$2I$$ respectively about their axis of rotation. If their kinetic energies of rotation are equal, their angular momenta will be in the ratio
A
$$1:2$$
B
$$\sqrt 2 :1$$
C
$$2:1$$
D
$$1:\sqrt 2 $$
Answer :
$$1:\sqrt 2 $$
48. The moment of inertia of a thin uniform rod of mass $$M$$ and length $$L$$ about an axis passing through its mid-point and perpendicular to its length is $${I_0}.$$ Its moment of inertia about an axis passing through one of its ends and perpendicular to its length is
A
$${I_0} + \frac{{M{L^2}}}{4}$$
B
$${I_0} + 2M{L^2}$$
C
$${I_0} + M{L^2}$$
D
$${I_0} + \frac{{M{L^2}}}{2}$$
Answer :
$${I_0} + \frac{{M{L^2}}}{4}$$
49. Consider a uniform square plate of side $$‘a’$$ and mass $$‘m’.$$ The moment of inertia of this plate about an axis perpendicular to its plane and passing through one of its comers is-
A
$$\frac{5}{6}m{a^2}$$
B
$$\frac{1}{12}m{a^2}$$
C
$$\frac{7}{12}m{a^2}$$
D
$$\frac{2}{3}m{a^2}$$
Answer :
$$\frac{2}{3}m{a^2}$$
50. The ratio of the accelerations for a solid sphere (mass $$m$$ and radius $$R$$ ) rolling down an incline of angle $$\theta $$ without slipping and slipping down the incline without rolling is
A
$$5:7$$
B
$$2:3$$
C
$$2:5$$
D
$$7:5$$
Answer :
$$5:7$$