71.
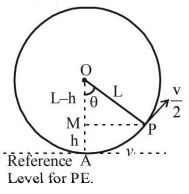
A bob of mass $$M$$ is suspended by a massless string of length $$L .$$ The horizontal velocity $$v$$ at position $$A$$ is just sufficient to make it reach the point $$B.$$ The angle $$\theta $$ at which the speed of the bob is half of that at $$A,$$ satisfies
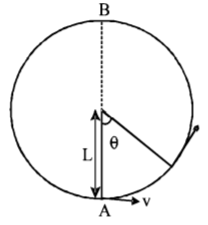
A
$$\theta = \frac{\pi }{4}$$
B
$$\frac{\pi }{4} < \theta < \frac{\pi }{2}$$
C
$$\frac{\pi }{2} < \theta < \frac{{3\pi }}{4}$$
D
$$\frac{{3\pi }}{4} < \theta < \pi $$
Answer :
$$\frac{{3\pi }}{4} < \theta < \pi $$
72. $$\left( {n - 1} \right)$$ equal point masses each of mass $$m$$ are placed at the vertices of a regular $$n$$-polygon. The vacant vertex has a position vector $$a$$ with respect to the centre of the polygon. The position vector of centre of mass is
A
$$ - \frac{1}{{\left( {n - 1} \right)}}a$$
B
$$\frac{a}{{\left( {n + 1} \right)}}$$
C
$$\frac{a}{n}$$
D
$$\frac{n}{{a + 1}}$$
Answer :
$$ - \frac{1}{{\left( {n - 1} \right)}}a$$
73. A system consists of three particles, each of mass $$m$$ and located at $$\left( {1,1} \right),\left( {2,2} \right)$$ and $$\left( {3,3} \right).$$ The coordinates of the centre of mass are
A
$$\left( {1,1} \right)$$
B
$$\left( {2,2} \right)$$
C
$$\left( {3,3} \right)$$
D
$$\left( {6,6} \right)$$
Answer :
$$\left( {2,2} \right)$$
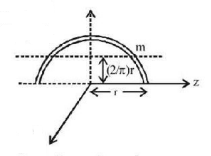
74. The moment of inertia of a uniform semicircular wire of mass $$m$$ and radius $$r,$$ about an axis passing through its centre of mass and perpendicular to its plane is $$m{r^2}\left( {1 - \frac{k}{{{\pi ^2}}}} \right)$$ then find the value of $$k.$$
A
2
B
3
C
4
D
5
Answer :
4
75. Moment of inertia of a circular wire of mass $$M$$ and radius $$R$$ about its diameter is-
A
$$\frac{{M{R^2}}}{2}$$
B
$$M{R^2}$$
C
$$2M{R^2}$$
D
$$\frac{{M{R^2}}}{4}$$
Answer :
$$\frac{{M{R^2}}}{2}$$
76. A particle of mass $$M$$ is revolving along a circle of radius $$R$$ and another particle of mass $$m$$ is revolving in a circle of radius $$r.$$ If time periods of both particles are same, then the ratio of their angular velocities is
A
$$1$$
B
$$\frac{R}{r}$$
C
$$\frac{r}{R}$$
D
$$\sqrt {\frac{R}{r}} $$
Answer :
$$1$$
77. A solid sphere is rotating in free space. If the radius of the sphere is increased keeping mass same which one of the following will not be affected?
A
Angular velocity
B
Angular momentum
C
Moment of inertia
D
Rotational kinetic energy
Answer :
Angular momentum
78.
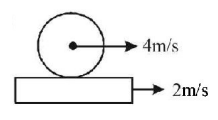
A cylinder $$A$$ rolls without slipping on a plank $$B.$$ The velocities of center of the cylinder and that of the plank are $$4\,m/s$$ and $$2\,m/s$$ respectively in same direction, with respect to the ground. Find the angular velocity of the cylinder (in $$rad/s$$ ) if its radius is $$1m.$$
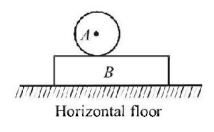
A
$$2\,rad/\sec $$
B
$$4\,rad/\sec $$
C
$$6\,rad/\sec $$
D
$$10\,rad/\sec $$
Answer :
$$2\,rad/\sec $$
79.
The moment of inertia of the rectangular plate $$ABCD,\left( {AB = 2\,BC} \right)$$ is minimum along the axis
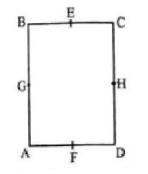
A
$$GH$$
B
$$EF$$
C
$$BC$$
D
$$AC$$
Answer :
$$EF$$
80. Moment of inertia of a hollow cylinder of mass $$M$$ and radius $$r$$ about its own axis is
A
$$\frac{2}{3}M{r^2}$$
B
$$\frac{2}{5}M{r^2}$$
C
$$\frac{1}{3}M{r^2}$$
D
$$M{r^2}$$
Answer :
$$M{r^2}$$