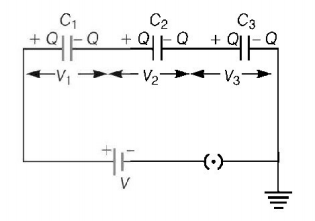
31. A parallel plate condenser with a dielectric of dielectric constant $$K$$ between the plates has a capacity $$C$$ and is charged to a potential $$V$$ volt. The dielectric slab is slowly removed from between the plates and then reinserted. The net work done by the system in this process is
A
zero
B
$$\frac{1}{2}\left( {K - 1} \right)C{V^2}$$
C
$$\frac{{C{V^2}\left( {K - 1} \right)}}{K}$$
D
$$\left( {K - 1} \right)C{V^2}$$
Answer :
zero
32. Capacitance (in $$F$$) of a spherical conductor with radius $$1m$$ is
A
$$1.1 \times {10^{ - 10}}$$
B
$${10^{ - 6}}$$
C
$$9 \times {10^{ - 9}}$$
D
$${10^{ - 3}}$$
Answer :
$$1.1 \times {10^{ - 10}}$$
33. A parallel plate capacitor with air between the plates is charged to a potential difference of $$500\,V$$ and then insulated. A plastic plate is inserted between the plates filling the whole gap. The potential difference between the plates now becomes $$75\,V.$$ The dielectric constant of plastic is
A
$$\frac{{10}}{3}$$
B
$$5$$
C
$$\frac{{20}}{3}$$
D
$$10$$
Answer :
$$\frac{{20}}{3}$$
34. The energy required to charge a parallel plate condenser of plate separation $$d$$ and plate area of cross-section $$A$$ such that the uniform electric field between the plates is $$E,$$ is
A
$${ \in _0}{E^2}Ad$$
B
$$\frac{1}{2}{ \in _0}{E^2}Ad$$
C
$$\frac{1}{2}{ \in _0}\frac{{{E^2}}}{{Ad}}$$
D
$${ \in _0}\frac{{{E^2}}}{{Ad}}$$
Answer :
$${ \in _0}{E^2}Ad$$
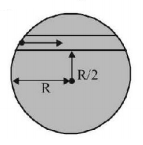
35.
A unit positive point charge of mass $$m$$ is projected with a velocity $$V$$ inside the tunnel as shown. The tunnel has been made inside a uniformly charged nonconducting sphere (charge density $$\rho $$), The minimum velocity with which the point charge should be projected such that it can reach the opposite end of the tunnel is equal to
A
$${\left[ {\frac{{\rho {R^2}}}{{4m{\varepsilon _0}}}} \right]^{\frac{1}{2}}}$$
B
$${\left[ {\frac{{\rho {R^2}}}{{24m{\varepsilon _0}}}} \right]^{\frac{1}{2}}}$$
C
$${\left[ {\frac{{\rho {R^2}}}{{6m{\varepsilon _0}}}} \right]^{\frac{1}{2}}}$$
D
zero because the initial and the final points are at same potential
Answer :
$${\left[ {\frac{{\rho {R^2}}}{{4m{\varepsilon _0}}}} \right]^{\frac{1}{2}}}$$
36. Three capacitors each of capacitance $$C$$ and of breakdown voltage $$V$$ are joined in series. The capacitance and breakdown voltage of the combination will be
A
$$\frac{C}{3},\frac{V}{3}$$
B
$$3C,\frac{V}{3}$$
C
$$\frac{C}{3},3V$$
D
$$3C,3V$$
Answer :
$$\frac{C}{3},3V$$
37. Two identical capacitors, have the same capacitance $$C.$$ One of them is charged to potential $${V_1}$$ and the other $${V_2}.$$ The negative ends of the capacitors are connected together. When the positive ends are also connected, the decrease in energy of the combined system is
A
$$\frac{1}{4}C\left( {V_1^2 - V_2^2} \right)$$
B
$$\frac{1}{4}C\left( {V_1^2 + V_2^2} \right)$$
C
$$\frac{1}{4}C{\left( {{V_1} - {V_2}} \right)^2}$$
D
$$\frac{1}{4}C{\left( {{V_1} + {V_2}} \right)^2}$$
Answer :
$$\frac{1}{4}C{\left( {{V_1} - {V_2}} \right)^2}$$
38. A capacitor of capacity $${C_1}$$ is charged upto $$V\,volt$$ and then connected to an uncharged capacitor of capacity $${C_2}.$$ Then final potential difference across each will be
A
$$\frac{{{C_2}V}}{{{C_1} + {C_2}}}$$
B
$$\left( {1 + \frac{{{C_2}}}{{{C_1}}}} \right)V$$
C
$$\frac{{{C_1}V}}{{{C_1} + {C_2}}}$$
D
$$\left( {1 - \frac{{{C_2}}}{{{C_1}}}} \right)V$$
Answer :
$$\frac{{{C_1}V}}{{{C_1} + {C_2}}}$$
39. The work done in placing a charge of $$8 \times {10^{ - 18}}$$ coulomb on a condenser of capacity 100 micro-farad is
A
$$16 \times {10^{ - 32}}joule$$
B
$$3.1 \times {10^{ - 26}}joule$$
C
$$4 \times {10^{ - 10}}joule$$
D
$$32 \times {10^{ - 32}}joule$$
Answer :
$$32 \times {10^{ - 32}}joule$$
40. If there are $$n$$ capacitors in parallel connected to $$V$$ volt source, then the energy stored is equal to
A
$$CV$$
B
$$\frac{1}{2}nC{V^2}$$
C
$$C{V^2}$$
D
$$\frac{1}{{2n}}C{V^2}$$
Answer :
$$\frac{1}{2}nC{V^2}$$