91. Five cells each of emf $$E$$ and internal resistance $$r$$ send the same amount of current through an external resistance $$R$$ whether the cells are connected in parallel or in series. Then the ratio $$\left( {\frac{R}{r}} \right)$$ is
A
2
B
$$\frac{1}{2}$$
C
$$\frac{1}{5}$$
D
1
Answer :
1
92. The masses of the three wires of copper are in the ratio of $$1:3:5$$ and their lengths are in the ratio of $$5 : 3: 1.$$ The ratio of their electrical resistance is
A
$$1:3:5$$
B
$$5:3:1$$
C
$$1:25:125$$
D
$$125:45:3$$
Answer :
$$125:45:3$$
93.
If power dissipated in the $$9\,\Omega $$ resistor in the circuit shown is $$36\,W,$$ the potential difference across the $$2\,\Omega $$ resistor is
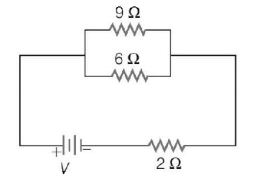
A
$$8\,V$$
B
$$10\,V$$
C
$$2\,V$$
D
$$4\,V$$
Answer :
$$10\,V$$
94. Direct current is passed through a copper sulphate solution using platinum electrodes. The elements liberated at the electrodes are
A
copper at anode and sulphur at cathode
B
sulphur at anode and copper at cathode
C
oxygen at anode and copper at cathode
D
copper at anode and oxygen at cathode
Answer :
oxygen at anode and copper at cathode
95. $$n$$ resistances each of $$r$$ ohm, when connected in parallel give an equivalent resistance of $$R$$ ohm. If these resistances were connected in series, the combination would have a resistance in ohms, equal to
A
$${n^2}R$$
B
$$\frac{R}{{{n^2}}}$$
C
$$\frac{R}{n}$$
D
$$nR$$
Answer :
$${n^2}R$$
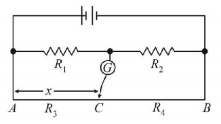
96.
In the shown arrangement of the experiment of the meter bridge if $$AC$$ corresponding to null deflection of galvanometer is $$x,$$ what would be its value if the radius of the wire $$AB$$ is doubled?
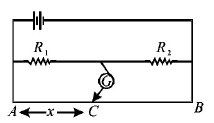
A
$$x$$
B
$$4x$$
C
$$\frac{x}{4}$$
D
$$2x$$
Answer :
$$x$$
97. It takes $$12$$ minutes to boil $$1$$ litre of water in an electric kettle. Due to some defect it becomes necessary to remove $$20\% $$ turns of heating coil of the kettle. After repair, how much time will it take to boil $$1$$ litre of water ?
A
9.6 minute
B
14.4 minute
C
16.8 minute
D
18.2 minute
Answer :
9.6 minute
98. The charge flowing through a resistance $$R$$ varies with time $$t$$ as $$Q = at - b{t^2}.$$ The total heat produced in $$R$$ by the time current ceases is
A
$$\frac{{{a^3}R}}{{6b}}$$
B
$$\frac{{{a^3}R}}{{3b}}$$
C
$$\frac{{{a^3}R}}{{2b}}$$
D
$$\frac{{{a^3}R}}{{b}}$$
Answer :
$$\frac{{{a^3}R}}{{6b}}$$
99. The thermo e.m.f. of a thermo -couple is $$25\mu \,V{/^ \circ }C$$ at room temperature. A galvanometer of $$40 \,ohm$$ resistance, capable of detecting current as low as $${10^{ - 5}}A,$$ is connected with the thermo couple. The smallest temperature difference that can be detected by this system is
A
$${16^ \circ }C$$
B
$${12^ \circ }C$$
C
$${8^ \circ }C$$
D
$${20^ \circ }C$$
Answer :
$${16^ \circ }C$$
100. Faraday’s laws are consequence of conservation of
A
energy
B
energy and magnetic field
C
charge
D
magnetic field
Answer :
energy