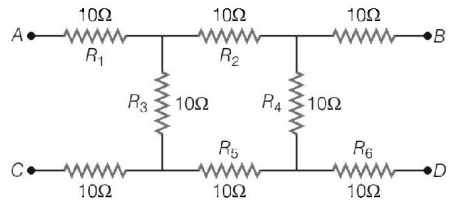
121.
What will be the equivalent resistance of circuit shown in figure between two points $$A$$ and $$D$$ ?

A
$$10\,\Omega $$
B
$$20\,\Omega $$
C
$$30\,\Omega $$
D
$$40\,\Omega $$
Answer :
$$30\,\Omega $$
122. Two metal wires of identical dimensions are connected in series. If $${\sigma _1}$$ and $${\sigma _2}$$ are the conductivities of the metal wires respectively, the effective conductivity of the combination is
A
$$\frac{{2{\sigma _1}{\sigma _2}}}{{{\sigma _1} + {\sigma _2}}}$$
B
$$\frac{{{\sigma _1} + {\sigma _2}}}{{2{\sigma _1}{\sigma _2}}}$$
C
$$\frac{{{\sigma _1} + {\sigma _2}}}{{{\sigma _1}{\sigma _2}}}$$
D
$$\frac{{{\sigma _1}{\sigma _2}}}{{{\sigma _1} + {\sigma _2}}}$$
Answer :
$$\frac{{2{\sigma _1}{\sigma _2}}}{{{\sigma _1} + {\sigma _2}}}$$
123. A constant voltage is applied between the two ends of a uniform metallic wire. Some heat is developed in it. The heat developed is doubled if
A
both the length and the radius of the wire are halved.
B
both the length and the radius of the wire are doubled.
C
the radius of the wire is doubled.
D
the length of the wire is doubled.
Answer :
both the length and the radius of the wire are doubled.
124. A metal wire is subjected to a constant potential difference. When the temperature of the metal wire increases, the drift velocity of the electron in it
A
increases, thermal velocity of the electron increases
B
decreases, thermal velocity of the electron increases
C
increases, thermal velocity of the electron decreases
D
decreases, thermal velocity of the electron decreases
Answer :
decreases, thermal velocity of the electron increases
125. When $$5V$$ potential difference is applied across a wire of length $$0.1\,m,$$ the drift speed of electrons is $$2.5 \times {10^{ - 4}}m{s^{ - 1}}.$$ If the electron density in the wire is $$8 \times {10^{28}}m{s^{ - 3}},$$ the resistivity of the material is close to :
A
$$1.06 \times {10^{ - 6}}\Omega m$$
B
$$1.06 \times {10^{ - 5}}\Omega m$$
C
$$1.06 \times {10^{ - 8}}\Omega m$$
D
$$1.06 \times {10^{ - 7}}\Omega m$$
Answer :
$$1.06 \times {10^{ - 5}}\Omega m$$
126. A current of $$2\,A,$$ passing through a conductor produces $$80\,J$$ of heat in $$10\,s.$$ The resistance of the conductor in ohm is
A
0.5
B
2
C
4
D
20
Answer :
2
127. A $$4\,\mu F$$ capacitor, a resistance of $$2.5\,M\Omega $$ is in series with $$12\,V$$ battery. Find the time after which the potential difference across the capacitor is 3 times the potential difference across the resistor. [Given l$$n\left( 2 \right) = 0.693$$ ]
A
$$13.86s$$
B
$$6.93s$$
C
$$7s$$
D
$$14s$$
Answer :
$$13.86s$$
128. The total momentum of electrons in a straight wire of length $$1000\,m$$ carrying a current of $$70A$$ is closest to
A
$$40 \times {10^{ - 8}}N - \sec $$
B
$$30 \times {10^{ - 8}}N - \sec $$
C
$$50 \times {10^{ - 8}}N - \sec $$
D
$$70 \times {10^{ - 8}}N - \sec $$
Answer :
$$40 \times {10^{ - 8}}N - \sec $$
129.
Each of the resistors shown in Fig. has resistance $$R.$$ Find the equivalent resistance between $$A$$ and $$B.$$

A
$$\frac{{7R}}{4}$$
B
$$\frac{{5R}}{4}$$
C
$$\frac{{9R}}{4}$$
D
$$\frac{{11R}}{4}$$
Answer :
$$\frac{{11R}}{4}$$
130. The amount of charge $$Q$$ passed in time $$t$$ through a cross-section of a wire is $$Q = 5{t^2} + 3t + 1.$$ The value of current at time $$t = 5\,s$$ is
A
$$9\,A$$
B
$$49\,A$$
C
$$53\,A$$
D
None of these
Answer :
$$53\,A$$