151.
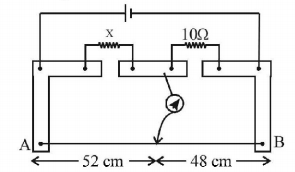
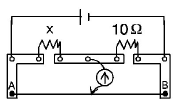
A meter bridge is set up as shown, to determine an unknown
resistance $$'X'$$ using a standard $$10\,ohm$$ resistor. The galvanometer shows null point when tapping-key is at $$52\,cm$$ mark. The end-corrections are $$1\,cm$$ and $$2\,cm$$ respectively for the ends $$A$$ and $$B.$$ The determined value of $$'X'$$ is
A
$$10.2\,ohm$$
B
$$10.6\,ohm$$
C
$$10.8\,ohm$$
D
$$11.1\,ohm$$
Answer :
$$10.6\,ohm$$
152.
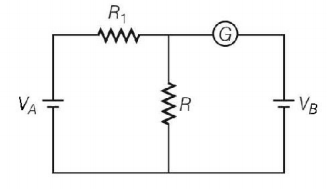
In the circuit shown, the cells $$A$$ and $$B$$ have negligible resistances. For $${V_A} = 12\,V,{R_1} = 500\,\Omega $$ and $$R = 100\,\Omega $$ the galvanometer $$\left( G \right)$$ shows no deflection. The value of $${V_B}$$ is
A
$$4\,V$$
B
$$2\,V$$
C
$$12\,V$$
D
$$6\,V$$
Answer :
$$2\,V$$
153. At room temperature, copper has free electron density of $$8.4 \times {10^{28}}$$ per $${m^3}.$$ The copper conductor has a cross-section of $${10^{ - 6}}{m^2}$$ and carries a current of $$5.4\,A.$$ The electron drift velocity in copper is
A
$$400\,m/s$$
B
$$0.4\,m/s$$
C
$$0.4\,mm/s$$
D
$$72\,m/s$$
Answer :
$$0.4\,mm/s$$
154. Three resistances each of $$4\,\Omega $$ are connected to form a triangle. The resistance between any two terminals is
A
$$12\,\Omega $$
B
$$2\,\Omega $$
C
$$6\,\Omega $$
D
$$\frac{8}{3}\,\Omega $$
Answer :
$$\frac{8}{3}\,\Omega $$
155. Forty electric bulbs are connected in series across a $$220\,V$$ supply. After one bulb is fused the remaining $$39$$ are connected again in series across the same supply. The illumination will be
A
more with $$40$$ bulbs than with $$39$$
B
more with $$39$$ bulbs than with $$40$$
C
equal in both the cases
D
in the ratio $${40^2}:{39^2}$$
Answer :
more with $$39$$ bulbs than with $$40$$
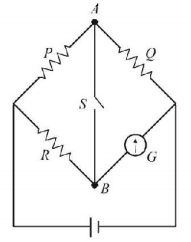
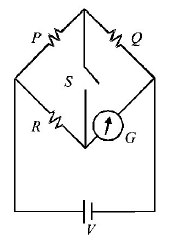
156.
In the circuit $$P \ne R$$ the reading of the galvanometer is same with switch $$S$$ open or closed. Then
A
$${I_R} = {I_G}$$
B
$${I_P} = {I_G}$$
C
$${I_Q} = {I_G}$$
D
$${I_Q} = {I_R}$$
Answer :
$${I_R} = {I_G}$$
157.
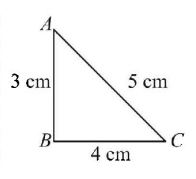
A $$12\,cm$$ wire is given a shape of a right angled triangle $$ABC$$ having sides $$3\,cm,4\,cm$$ and $$5\,cm$$ as shown in the figure. The resistance between two ends $$\left( {AB,BC,CA} \right)$$ of the respective sides are measured one by one by a multi-meter. The
resistances will be in the ratio of
A
$$3:4:5$$
B
$$9:16:25$$
C
$$27:32:35$$
D
$$21:24:25$$
Answer :
$$27:32:35$$
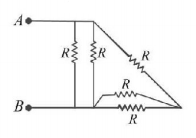
158.
In the given mesh, each resistor has resistance $$R.$$ The effective resistance between the terminals $$A$$ and $$B$$ is
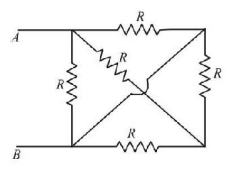
A
$$\frac{{3R}}{8}$$
B
$$\frac{{R}}{2}$$
C
$$R$$
D
$$2\,R$$
Answer :
$$\frac{{3R}}{8}$$
159. Drift velocity of electrons is due to
A
motion of conduction electrons due to random collisions.
B
motion of conduction electrons due to electric field $$\vec E.$$
C
repulsion to the conduction electrons due to inner electrons of ions.
D
collision of conduction electrons with each other.
Answer :
motion of conduction electrons due to electric field $$\vec E.$$
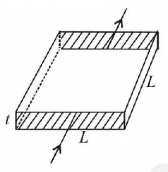
160.
Consider a thin square sheet of side $$L$$ and thickness $$t,$$ made of a material of resistivity $$\rho .$$ The resistance between two opposite faces, shown by the shaded areas in the figure is
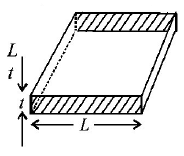
A
directly proportional to $$L$$
B
directly proportional to $$t$$
C
independent of $$L$$
D
independent of $$t$$
Answer :
independent of $$L$$