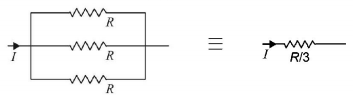261. Let $$C$$ be the capacitance of a capacitor discharging through a resistor $$R.$$ Suppose $${t_1}$$ is the time taken for the energy stored in the capacitor to reduce to half its initial value and $${t_2}$$ is the time taken for the charge to reduce to one-fourth its initial value. Then the ratio $$\frac{{{t_1}}}{{{t_2}}}$$ will be
A
1
B
$$\frac{1}{2}$$
C
$$\frac{1}{4}$$
D
2
Answer :
$$\frac{1}{4}$$
262.
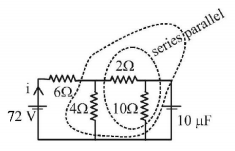
Determine the charge on the capacitor in the following circuit:
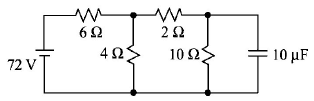
A
$$60\mu C$$
B
$$2\mu C$$
C
$$10\mu C$$
D
$$200\mu C$$
Answer :
$$200\mu C$$
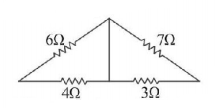
263.
The three resistance of equal value are arranged in the different combinations shown below. Arrange them in increasing order of power dissipation.
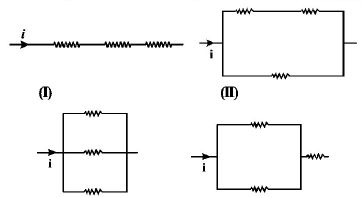
A
$$III < II < IV < I$$
B
$$II < III < IV < I$$
C
$$I < IV < III < II$$
D
$$I < III < II < IV$$
Answer :
$$III < II < IV < I$$
264.
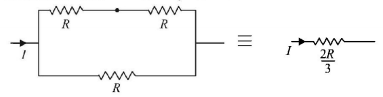
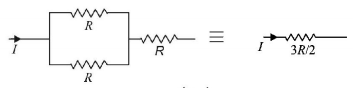
In the given network of four resistances, the equivalent resistance is:
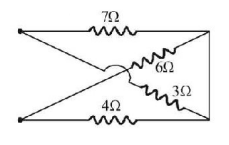
A
$$20\,\Omega $$
B
$$5.4\,\Omega $$
C
$$12\,\Omega $$
D
$$4.5\,\Omega $$
Answer :
$$4.5\,\Omega $$
265. The resistance of a wire is $$R.$$ It is bent at the middle by $${180^ \circ }$$ and both the ends are twisted together to make a shorter wire. The resistance of the new wire is
A
$$2R$$
B
$$\frac{R}{2}$$
C
$$\frac{R}{4}$$
D
$$\frac{R}{8}$$
Answer :
$$\frac{R}{4}$$
266. The current density varies with radial distance $$r$$ as $$J = a{r^2},$$ in a cylindrical wire of radius $$R.$$ The current passing through the wire between radial distance $$\frac{R}{3}$$ and $$\frac{R}{2}$$ is
A
$$\frac{{65\pi a{R^4}}}{{2592}}$$
B
$$\frac{{25\pi a{R^4}}}{{72}}$$
C
$$\frac{{65\pi {a^2}{R^3}}}{{2938}}$$
D
$$\frac{{81\pi {a^2}{R^4}}}{{144}}$$
Answer :
$$\frac{{65\pi a{R^4}}}{{2592}}$$
267. $$n$$ equal resistors are first connected in series and then connected in parallel. What is the ratio of the maximum to the minimum resistance?
A
$$n$$
B
$$\frac{1}{{{n^2}}}$$
C
$${{n^2}}$$
D
$$\frac{1}{n}$$
Answer :
$${{n^2}}$$
268. The internal resistance of a $$2.1\,V$$ cell which gives a current of $$0.2\,A$$ through a resistance of $$10\,\Omega $$ is
A
$$0.2\,\Omega $$
B
$$0.5\,\Omega $$
C
$$0.8\,\Omega $$
D
$$1.0\,\Omega $$
Answer :
$$0.5\,\Omega $$