61. Two batteries with e.m.f. $$12\,V$$ and $$13\,V$$ are connected in parallel across a load resistor of $$10\,\Omega $$. The internal resistances of the two batteries are $$1\,\Omega $$ and $$2\,\Omega $$ respectively. The voltage across the load lies between :
A
$$11.6\,V$$ and $$11.7\,V$$
B
$$11.5\,V$$ and $$11.6\,V$$
C
$$11.4\,V$$ and $$11.5\,V$$
D
$$11.7\,V$$ and $$11.8\,V$$
Answer :
$$11.5\,V$$ and $$11.6\,V$$
62. A $$4\mu F$$ conductor is charged to $$400\,V$$ and then its plates are joined through a resistance of $$1\,k\Omega .$$ The heat produced in the resistance is
A
$$0.16\,J$$
B
$$1.28\,J$$
C
$$0.64\,J$$
D
$$0.32\,J$$
Answer :
$$0.32\,J$$
63.
In the given circuit, it is observed that the current $$I$$ is independent of the value of the resistance $${R_6}.$$ Then the resistance values must satisfy
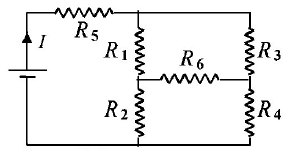
A
$${R_1}{R_2}{R_5} = {R_3}{R_4}{R_6}$$
B
$$\frac{1}{{{R_5}}} + \frac{1}{{{R_6}}} = \frac{1}{{{R_1} + {R_2}}} + \frac{1}{{{R_3} + {R_4}}}$$
C
$${R_1}{R_4} = {R_2}{R_3}$$
D
$${R_1}{R_3} = {R_2}{R_4} = {R_5}{R_6}$$
Answer :
$${R_1}{R_4} = {R_2}{R_3}$$
64. If an ammeter is to be used in place of a voltmeter, then we must connect with the ammeter a
A
low resistance in parallel
B
high resistance in parallel
C
high resistance in series
D
low resistance in series.
Answer :
high resistance in series
65. A potentiometer is an accurate and versatile device to make electrical measurement of EMF because the method involves
A
cells
B
potential gradients
C
a condition of no current flow through the galvanometer
D
a combination of cells, galvanometer and resistances
Answer :
a condition of no current flow through the galvanometer
66. For a cell, the terminal potential difference is $$2.2\,V$$ when circuit is open and reduces to $$1.8\,V$$ when cell is connected to a resistance $$R = 5\,\Omega ,$$ the internal resistance $$\left( r \right)$$ of cell is
A
$$\frac{{10}}{9}\Omega $$
B
$$\frac{9}{{10}}\Omega $$
C
$$\frac{{11}}{9}\Omega $$
D
$$\frac{5}{9}\Omega $$
Answer :
$$\frac{{10}}{9}\Omega $$
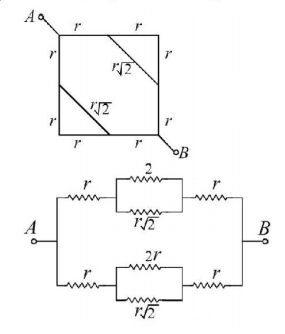
67.
A wire has linear resistance $$\rho $$ (in $$Ohm/m$$ ). Find the resistance $$R$$ between points $$A$$ and $$B$$ if the side of the larger square is $$'d'.$$
A
$$\frac{{\rho d}}{{\sqrt 2 }}$$
B
$$\sqrt 2 \rho d$$
C
$$2rd$$
D
None of these
Answer :
$$\frac{{\rho d}}{{\sqrt 2 }}$$
68.
The current $$i$$ in the circuit (see Fig) is

A
$$\frac{1}{{45}}A$$
B
$$\frac{1}{{15}}A$$
C
$$\frac{1}{{10}}A$$
D
$$\frac{1}{5}A$$
Answer :
$$\frac{1}{{10}}A$$
69.
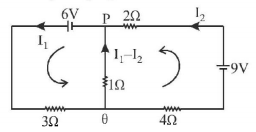
In the circuit shown, the current in the $$1\Omega $$ resistor is :
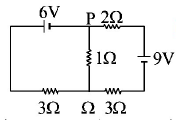
A
$$0.13\,A,$$ from $$Q$$ to $$P$$
B
$$0.13\,A,$$ from $$P$$ to $$Q$$
C
$$1.3\,A$$ from $$P$$ to $$Q$$
D
$$0\,A$$
Answer :
$$0.13\,A,$$ from $$Q$$ to $$P$$
70. The mean free path of electrons in a metal is $$4 \times {10^{ - 8}}m.$$ The electric field which can give on an average $$2\,eV$$ energy to an electron in the metal will be in unit of $$V{m^{ - 1}}$$
A
$$8 \times {10^7}$$
B
$$5 \times {10^{ - 11}}$$
C
$$8 \times {10^{ - 11}}$$
D
$$5 \times {10^7}$$
Answer :
$$5 \times {10^7}$$