71. A potentiometer wire has length $$4\,m$$ and resistance $$8\,\Omega .$$ The resistance that must be connected in series with the wire and an accumulator of emf $$2V,$$ so as to get a potential gradient $$1\,mV$$ per $$cm$$ on the wire is
A
$$32\,\Omega $$
B
$$40\,\Omega $$
C
$$44\,\Omega $$
D
$$48\,\Omega $$
Answer :
$$32\,\Omega $$
72. A student measures the terminal potential difference $$\left( V \right)$$ of a cell (of emf $$\varepsilon $$ and internal resistance $$r$$) as a function of the current $$\left( I \right)$$ flowing through it. The slope and intercept of the graph between $$V$$ and $$I,$$ respectively, equal to
A
$$\varepsilon \,{\text{and}}\, - r$$
B
$$ - r\,{\text{and}}\,\varepsilon $$
C
$$r\,{\text{and}}\, - \varepsilon $$
D
$$ - \varepsilon \,{\text{and}}\,r$$
Answer :
$$ - r\,{\text{and}}\,\varepsilon $$
73. The resistance of a wire is $$5\,ohm$$ at $${50^ \circ }C$$ and $$6\,ohm$$ at $${100^ \circ }C.$$ The resistance of the wire at $${0^ \circ }C$$ will be
A
$$3\,ohm$$
B
$$2\,ohm$$
C
$$1\,ohm$$
D
$$4\,ohm$$
Answer :
$$4\,ohm$$
74. A wire of a certain material is stretched slowly by 10 percent. Its new resistance and specific resistance become respectively
A
1.2 times, 1.1 times
B
1.21 times, same
C
Both remain the same
D
1.1 times, 1.1 times
Answer :
1.21 times, same
75. Drift speed of electrons, when $$1.5\,A$$ of current flows in a copper wire of cross section $$5m{m^2},$$ is $$v.$$ If the electron density in copper is $$9 \times {10^{28}}/{m^3}$$ the value of $$v$$ in mm/s close to (Take charge of electron to be = $$1.6 \times {10^{ - 19}}C$$ )
A
0.02
B
3
C
2
D
0.2
Answer :
0.02
76. In meter bridge, the balancing length from left is found to be $$20\,cm$$ when standard resistance of $$1\,\Omega $$ is in right gap. The value of unknown resistance is
A
$$0.25\,\Omega $$
B
$$0.4\,\Omega $$
C
$$0.5\,\Omega $$
D
$$4\,\Omega $$
Answer :
$$0.25\,\Omega $$
77.
A current of $$3\,A$$ flows through the $$2\,\Omega $$ resistor shown in the circuit. The power dissipated in the $$5\,\Omega $$ resistor is

A
$$4\,W$$
B
$$2\,W$$
C
$$1\,W$$
D
$$5\,W$$
Answer :
$$5\,W$$
78. If $${\theta _i},$$ is the inversion temperature, $${\theta _n}$$ is the neutral temperature, $${\theta _c}$$ , is the temperature of the cold junction, then
A
$${\theta _i} + {\theta _c} = {\theta _n}$$
B
$${\theta _i} - {\theta _c} = 2{\theta _n}$$
C
$$\frac{{{\theta _i} + {\theta _C}}}{2} = {\theta _n}$$
D
$${\theta _c} - {\theta _i} = 2{\theta _n}$$
Answer :
$$\frac{{{\theta _i} + {\theta _C}}}{2} = {\theta _n}$$
79.
A circuit is connected as shown in the figure with the switch $$S$$ open. When the switch is closed, the total amount of charge that flows from $$Y$$ to $$X$$ is
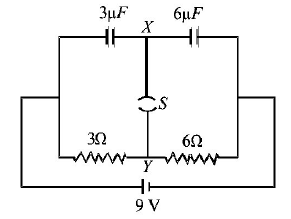
A
0
B
$$54\mu C$$
C
$$27\mu C$$
D
$$81\mu C$$
Answer :
$$27\mu C$$
80. 40 electric bulbs are connected in series across a $$220\,V$$ supply. After one bulb is fused the remaining 39 are connected again in series across the same supply. The illumination will be
A
more with 40 bulbs than with 39
B
more with 39 bulbs than with 40
C
equal in both the cases
D
in the ratio $${40^2}:{39^2}$$
Answer :
more with 39 bulbs than with 40