31.
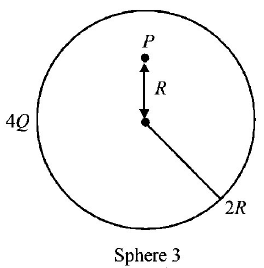
Charges $$Q, 2Q$$ and $$4Q$$ are uniformly distributed in three dielectric solid spheres 1, 2 and 3 of radii $$\frac{R}{2},$$ $$R$$ and $$2R$$ respectively, as shown in figure. If magnitude of the electric fields at point $$P$$ at a distance $$R$$ from the centre of sphere 1, 2 and 3 are $${E_1},{E_2}$$ and $${E_3}$$ respectively, the

A
$${E_1} > {E_2} > {E_3}$$
B
$${E_3} > {E_1} > {E_2}$$
C
$${E_2} > {E_1} > {E_3}$$
D
$${E_3} > {E_2} > {E_1}$$
Answer :
$${E_2} > {E_1} > {E_3}$$
32.
The region between two concentric spheres of radii $$'a'$$ and $$'b',$$ respectively (see figure), have volume charge density $$r = \frac{A}{r},$$ where $$A$$ is a constant and $$r$$ is the distance from the centre. At the centre of the spheres is a point charge $$Q.$$ The value of $$A$$ such that the electric field in the region between the spheres will be constant, is :

A
$$\frac{{2Q}}{{p\left( {{a^2} - {b^2}} \right)}}$$
B
$$\frac{{2Q}}{{p{a^2}}}$$
C
$$\frac{Q}{{2p{a^2}}}$$
D
$$\frac{Q}{{2p\left( {{b^2} - {a^2}} \right)}}$$
Answer :
$$\frac{Q}{{2p{a^2}}}$$
33. A charge $$q$$ is placed at the corner of a cube of side $$a.$$ The electric flux through the cube is
A
$$\frac{q}{{{\varepsilon _0}}}$$
B
$$\frac{q}{{3{\varepsilon _0}}}$$
C
$$\frac{q}{{6{\varepsilon _0}}}$$
D
$$\frac{q}{{8{\varepsilon _0}}}$$
Answer :
$$\frac{q}{{8{\varepsilon _0}}}$$
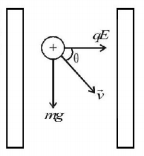
34. Two large vertical and parallel metal plates having a separation of $$1cm$$ are connected to a $$DC$$ voltage source of potential difference $$X.$$ A proton is released at rest midway between the two plates. It is found to move at $${45^ \circ }$$ to the vertical JUST after release. Then $$X$$ is nearly
A
$$1 \times {10^{ - 5}}V$$
B
$$1 \times {10^{ - 7}}V$$
C
$$1 \times {10^{ - 9}}V\,$$
D
$$1 \times {10^{ - 10}}V$$
Answer :
$$1 \times {10^{ - 9}}V\,$$
35. On decreasing the distance between the two charges of a dipole which is perpendicular to electric field and decreasing the angle between the dipole and electric field, the torque on the dipole
A
increases
B
decreases
C
remains same
D
cannot be predicted
Answer :
decreases
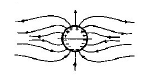
36. A long cylindrical shell carries positive surface charge $$\sigma $$ in the upper half and negative surface charge - $$\sigma $$ in the lower half. The electric field lines around the cylinder will look like figure given in : (figures are schematic and not drawn to scale)
A

B


C


D


Answer :


37.
Consider a system of three charges $$\frac{q}{3},\frac{q}{3}$$ and $$ - \frac{{2q}}{3}$$ placed at points $$A, B$$ and $$C,$$ respectively, as shown in the figure. Take $$O$$ to be the centre of the circle of radius $$R$$ and angle $$CAB = {60^ \circ }$$

A
The electric field at point $$O$$ is $$\frac{q}{{8\pi {\varepsilon _0}{R^2}}}$$ directed along the negative $$x$$-axis
B
The potential energy of the system is zero
C
The magnitude of the force between the charges at $$C$$ and $$B$$ is $$\frac{q^2}{{54\pi {\varepsilon _0}{R^2}}}$$
D
The potential at point $$O$$ is $$\frac{q}{{12\pi {\varepsilon _0}R}}$$
Answer :
The magnitude of the force between the charges at $$C$$ and $$B$$ is $$\frac{q^2}{{54\pi {\varepsilon _0}{R^2}}}$$
38.
A thin glassrod is bent into a semicircle of radius $$r.$$ A charge $$+Q$$ is uniformly distributed along the upper half, and a charge $$-Q$$ is uniformly distributed along the lower half, as shown in fig. The electric field $$E$$ at $$P,$$ the centre of the semicircle, is

A
$$\frac{Q}{{{\pi ^2}{\varepsilon _0}{r^2}}}$$
B
$$\frac{{2Q}}{{{\pi ^2}{\varepsilon _0}{r^2}}}$$
C
$$\frac{{4Q}}{{{\pi ^2}{\varepsilon _0}{r^2}}}$$
D
$$\frac{Q}{{4{\pi ^2}{\varepsilon _0}{r^2}}}$$
Answer :
$$\frac{Q}{{{\pi ^2}{\varepsilon _0}{r^2}}}$$
39.
Point charge $$q$$ moves from point $$P$$ to point $$S$$ along the path $$PQRS$$ (as shown in fig.) in a uniform electric field $$E$$ pointing co-parallel to the positive direction of $$X$$-axis.
The coordinates of the points $$P,Q,R$$ and $$S$$ are $$\left( {a,b,0} \right),\left( {2a,0,0} \right),\left( {a, - b,0} \right)$$ and $$\left( {0,0,0} \right)$$ respectively.
The workdone by the field in the above case is given by the expression

A
$$qEA$$
B
$$-qEA$$
C
$$qEA\sqrt 2 $$
D
$$qE\sqrt {\left[ {{{\left( {2a} \right)}^2} + {b^2}} \right]} $$
Answer :
$$-qEA$$
40. The total electric flux emanating from a closed surface enclosing an $$\alpha $$-particle is ($$e$$-electronic charge)
A
$$\frac{{2e}}{{{\varepsilon _0}}}$$
B
$$\frac{e}{{{\varepsilon _0}}}$$
C
$$e{\varepsilon _0}$$
D
$$\frac{{{\varepsilon _0}e}}{4}$$
Answer :
$$\frac{{2e}}{{{\varepsilon _0}}}$$