81. A point charge $$+ q$$ is placed at mid-point of a cube of side $$L.$$ The electric flux emerging from the cube is
A
$$\frac{q}{{{\varepsilon _0}}}$$
B
$$\frac{{6q{L^2}}}{{{\varepsilon _0}}}$$
C
$$\frac{q}{{6{L^2}{\varepsilon _0}}}$$
D
zero
Answer :
$$\frac{q}{{{\varepsilon _0}}}$$
82.
The electric field intensity at the centre of a uniformly charged hemispherical shell is $${E_0}.$$ Now two portions of the hemisphere are cut from either side, and the remaining portion is shown in Fig. If $$\alpha = \beta = \frac{\pi }{3},$$ then the electric field intensity at the centre due to the remaining portion is

A
$$\frac{{{E_0}}}{3}$$
B
$$\frac{{{E_0}}}{6}$$
C
$$\frac{{{E_0}}}{2}$$
D
information insufficient
Answer :
$$\frac{{{E_0}}}{2}$$
83. When an electric dipole $$\overrightarrow P $$ is placed in a uniform electric field $$\overrightarrow E $$ then at what angle between $$\overrightarrow P $$ and $$\overrightarrow E $$ the value of torque will be maximum?
A
$${90^ \circ }$$
B
$${0^ \circ }$$
C
$${180^ \circ }$$
D
$${45^ \circ }$$
Answer :
$${90^ \circ }$$
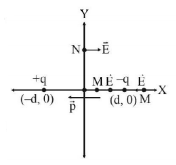
84. Two point charges $$ + q$$ and $$ - q$$ are held fixed at $$\left( { - d,o} \right)$$ and $$\left( {d,o} \right)$$ respectively of a $$x-y$$ coordinate system. Then
A
The electric field $$E$$ at all points on the $$x$$-axis has the same direction
B
Electric field at all points on $$y$$-axis is along $$x$$-axis
C
Work has to be done in bringing a test charge from $$\infty $$ to the origin
D
The dipole moment is $$2qd$$ along the $$x$$-axis
Answer :
Electric field at all points on $$y$$-axis is along $$x$$-axis
85. A charge $$q\,\mu C$$ is placed at the centre of a cube of a side $$0.1\,m,$$ then the electric flux diverging from each face of the cube is
A
$$\frac{{q \times {{10}^{ - 6}}}}{{24{\varepsilon _0}}}$$
B
$$\frac{{q \times {{10}^{ - 4}}}}{{{\varepsilon _0}}}$$
C
$$\frac{{q \times {{10}^{ - 6}}}}{{6{\varepsilon _0}}}$$
D
$$\frac{{q \times {{10}^{ - 4}}}}{{12{\varepsilon _0}}}$$
Answer :
$$\frac{{q \times {{10}^{ - 6}}}}{{6{\varepsilon _0}}}$$
86. If electric field in a region is radially outward with magnitude $$E = Ar,$$ the charge contained in a sphere of radius $$r$$ centred at the origin is
A
$$\frac{1}{{4\pi {\varepsilon _0}}}A{r^3}$$
B
$$4\pi {\varepsilon _0}A{r^3}$$
C
$$\frac{1}{{4\pi {\varepsilon _0}}}\frac{A}{{{r^3}}}$$
D
$$\frac{{4\pi {\varepsilon _0}A}}{{{r^3}}}$$
Answer :
$$4\pi {\varepsilon _0}A{r^3}$$
87. The number of electric lines of force that radiate outwards from one coulomb of charge in vacuum is
A
$$1.13 \times {10^{11}}$$
B
$$1.13 \times {10^{10}}$$
C
$$0.61 \times {10^{11}}$$
D
$$0.61 \times {10^9}$$
Answer :
$$1.13 \times {10^{11}}$$
88. The electric field intensity just sufficient to balance the earth’s gravitational attraction on an electron will be: (given mass and charge of an electron respectively are $$9.1 \times {10^{ - 31}}kg$$ and $$ - 1.6 \times {10^{ - 19}}C.$$ )
A
$$ - 5.6 \times {10^{ - 11}}N/C$$
B
$$ - 4.8 \times {10^{ - 15}}N/C$$
C
$$ - 1.6 \times {10^{ - 19}}N/C$$
D
$$ - 3.2 \times {10^{ - 19}}N/C$$
Answer :
$$ - 5.6 \times {10^{ - 11}}N/C$$
89.
In the figure the electric lines on the right have twice the separation of those on the left. If a charge particle takes time $$t$$ to move a distance $$x$$ in left region, then it will take time to travel the same distance in the right side region is :

A
$$\frac{t}{2}$$
B
$$t$$
C
$$\sqrt 2 t$$
D
$$2t$$
Answer :
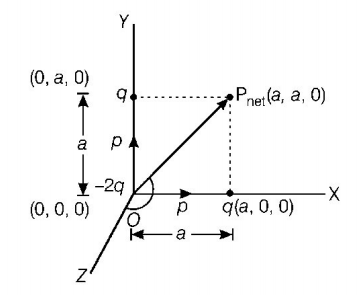
$$\sqrt 2 t$$
90. Three point charges $$+ q, - 2q$$ and $$+q$$ are placed at points $$\left( {x = 0,y = a,z = 0} \right),\left( {x = 0,y = 0,z = 0} \right)$$ and $$\left( {x = a,y = 0,z = 0} \right),$$ respectively. The magnitude and direction of the electric dipole moment vector of this charge assembly are
A
$$\sqrt 2 qa$$ along $$+y$$ direction
B
$$\sqrt 2 aq$$ along the line joining points $$\left( {x = 0,y = 0,z = 0} \right)$$ and $$\left( {x = a,y = a,z = 0} \right)$$
C
$$qa$$ along the line joining points $$\left( {x = 0,y = 0,z = 0} \right)$$ and $$\left( {x = a,y = a,z = 0} \right)$$
D
$$\sqrt 2 aq$$ along $$+ x$$ direction
Answer :
$$\sqrt 2 aq$$ along the line joining points $$\left( {x = 0,y = 0,z = 0} \right)$$ and $$\left( {x = a,y = a,z = 0} \right)$$