51. A charge of 3 coulomb moving in a uniform electric field experiences a force of 3000 newton. The potential difference between the two points situated in a field at a distance of $$1\,cm$$ from each other will be :
A
100
B
5000
C
10
D
50
Answer :
10
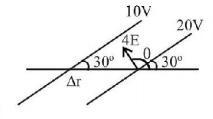
52.
Equipotential surfaces are shown in figure. Then the electric field strength will be
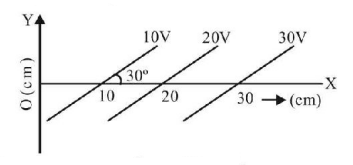
A
$$100\,V{m^{ - 1}}$$ along $$X$$-axis
B
$$100\,V{m^{ - 1}}$$ along $$Y$$-axis
C
$$200\,V{m^{ - 1}}$$ at an angle $${120^ \circ }$$ with $$X$$-axis
D
$$50\,V{m^{ - 1}}$$ at an angle $${120^ \circ }$$ with $$X$$-axis
Answer :
$$200\,V{m^{ - 1}}$$ at an angle $${120^ \circ }$$ with $$X$$-axis
53.
In the electric field of a point charge $$q,$$ a certain charge is carried from point $$A$$ to $$B,C,D$$ and $$E.$$ Then the work done is

A
least along the path $$AB$$
B
least along the path $$AD$$
C
zero along all the paths $$AB,AC,AD$$ and $$AE$$
D
least along $$AE$$
Answer :
zero along all the paths $$AB,AC,AD$$ and $$AE$$
54. If the electrostatic potential were given by $$\phi = {\phi _0}\left( {{x^2} + {y^2} + {z^2}} \right),$$ where $${\phi _0}$$ is constant, then the charge density giving rise to the above potential would be.
A
0
B
$$ - 6{\phi _0}{\varepsilon _0}$$
C
$$ - 2{\phi _0}{\varepsilon _0}$$
D
$$ - \frac{{6{\phi _0}}}{{{\varepsilon _0}}}$$
Answer :
$$ - 6{\phi _0}{\varepsilon _0}$$
55.
Three identical metallic uncharged spheres $$A,B$$ and $$C$$ each of radius $$a,$$ are kept at the corners of an equilateral triangle of side $$d\left( {d > > a} \right)$$ as shown in Fig. The fourth sphere (of radius $$a$$ ), which has a charge $$q,$$ touches $$A$$ and is then removed to a position far away. $$B$$ is earthed and then the earth connection is removed. $$C$$ is then earthed. The charge on $$C$$ is

A
$$\frac{{qa}}{{2d}}\left( {\frac{{2d - a}}{{2d}}} \right)$$
B
$$\frac{{qa}}{{2d}}\left( {\frac{{2d - a}}{d}} \right)$$
C
$$ - \frac{{qa}}{{2d}}\left( {\frac{{d - a}}{d}} \right)$$
D
$$\frac{{2qa}}{d}\left( {\frac{{d - a}}{{2d}}} \right)$$
Answer :
$$ - \frac{{qa}}{{2d}}\left( {\frac{{d - a}}{d}} \right)$$
56. A conducting sphere of radius $$R$$ is given a charge $$Q.$$ The electric potential and the electric field at the centre of the sphere respectively are
A
zero and $$\frac{Q}{{4\pi {\varepsilon _0}{R^2}}}$$
B
$$\frac{Q}{{4\pi {\varepsilon _0}R}}$$ and zero
C
$$\frac{Q}{{4\pi {\varepsilon _0}R}}{\text{and}}\frac{Q}{{4\pi {\varepsilon _0}{R^2}}}$$
D
Both and zero
Answer :
$$\frac{Q}{{4\pi {\varepsilon _0}R}}$$ and zero
57. Each corner of a cube of side $$l$$ has a negative charge, $$-q.$$ The electrostatic potential energy of a charge $$q$$ at the centre of the cube is
A
$$ - \frac{{4{q^2}}}{{\sqrt 2 \pi {\varepsilon _0}l}}$$
B
$$\frac{{\sqrt 3 {q^2}}}{{4\pi {\varepsilon _0}l}}$$
C
$$\frac{{4{q^2}}}{{\sqrt 2 \pi {\varepsilon _0}l}}$$
D
$$ - \frac{{4{q^2}}}{{\sqrt 3 \pi {\varepsilon _0}l}}$$
Answer :
$$ - \frac{{4{q^2}}}{{\sqrt 3 \pi {\varepsilon _0}l}}$$
58.
As per this diagram a point charge $$+q$$ is placed at the origin $$O.$$ Work done in taking another point charge $$- Q$$ from the point $$A$$ [coordinates $$\left( {0,a} \right)$$ ] to another point $$B$$ [coordinates $$\left( {a,0} \right)$$ ] along the straight path $$AB$$ is
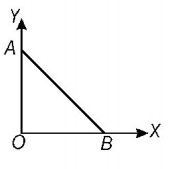
A
zero
B
$$\left( {\frac{{ - qQ}}{{4\pi {\varepsilon _0}}}\frac{1}{{{a^2}}}} \right)\sqrt 2 a$$
C
$$\left( {\frac{{qQ}}{{4\pi {\varepsilon _0}}}\frac{1}{{{a^2}}}} \right) \cdot \frac{a}{{\sqrt 2 }}$$
D
$$\left( {\frac{{qQ}}{{4\pi {\varepsilon _0}}}\frac{1}{{{a^2}}}} \right)\sqrt 2 a$$
Answer :
zero
59. Two concentric spheres of radii $$R$$ and $$r$$ have similar charges with equal surface charge densities $$\left( \sigma \right).$$ What is the electric potential at their common centre ?
A
$$\frac{\sigma }{{{\varepsilon _0}}}$$
B
$$\frac{\sigma }{{{\varepsilon _0}}}\left( {R - r} \right)$$
C
$$\frac{\sigma }{{{\varepsilon _0}}}\left( {R + r} \right)$$
D
None of these
Answer :
$$\frac{\sigma }{{{\varepsilon _0}}}\left( {R + r} \right)$$
60. An electric dipole, consisting of two opposite charges of $$2 \times {10^{ - 6}}C$$ each separated by a distance $$3\,cm$$ is placed in an electric field of $$2 \times {10^5}N/C.$$ Torque on the dipole is
A
$$12 \times {10^{ - 1}}N - m$$
B
$$12 \times {10^{ - 2}}N - m$$
C
$$12 \times {10^{ - 3}}N - m$$
D
$$12 \times {10^{ - 4}}N - m$$
Answer :
$$12 \times {10^{ - 3}}N - m$$