141. A current of $$1.5\,A$$ flows through a solenoid of length $$20.0\,cm,$$ cross-section $$20.0\,c{m^2}$$ and 400 turns. The current is suddenly switched off in a short time of 1.0 millisecond. Ignoring the variation in the magnetic field the ends, the average back emf induced in the solenoid is:
A
$$0.3\,V$$
B
$$9.6\,V$$
C
$$30.0\,V$$
D
$$3.0\,V$$
Answer :
$$0.3\,V$$
142.
An $$LCR$$ circuit is equivalent to a damped pendulum. In an
$$LCR$$ circuit the capacitor is charged to $${Q_0}$$ and then connected to the $$L$$ and $$R$$ as shown below :
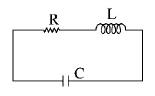
If a student plots graphs of the square of maximum charge
$$\left( {Q_{Max}^2} \right)$$ on the capacitor with time($$t$$) for two different values $${L_1}$$ and $${L_2}\left( {{L_1} > {L_2}} \right)$$ of $$L$$ then which of the following represents this graph correctly ? (plots are schematic and not drawn to scale)
A
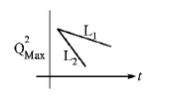

B
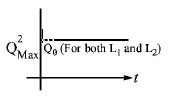

C
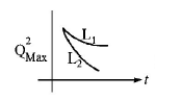

D
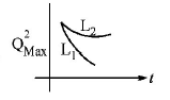

Answer :


143.
The figure shows a conducting loop consisting of half circle of area $$A = 0.06\,{m^2}$$ and three straight segments. The half circle lies in a uniform changing magnetic field $$B = 4{r^2} + 2t + 5$$ ($$SI$$ unit), where $$t$$ is the time in second. An ideal battery $$E = 2\,V$$ is connected as shown and the total resistance of the wire is $$2\Omega .$$ The net current in the loop is at $$t{\text{ }} = {\text{ }}5{\text{ second}}$$ is:
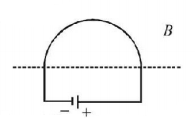
A
$$1\,A$$
B
$$1.5\,A$$
C
$$0.26\,A$$
D
$$0.10\,A$$
Answer :
$$0.26\,A$$
144. A boat is moving due east in a region where the earth's magnetic field is $$5.0 \times {10^{ - 5}}N{A^{ - 1}}{m^{ - 1}}$$ due north and horizontal. The boat carries a vertical aerial $$2\,m$$ long. If the speed of the boat is $$1.50\,m{s^{ - 1}}$$ the magnitude of the induced emf in the wire of aerial is
A
$$0.75\,mV$$
B
$$0.50\,mV$$
C
$$0.15\,mV$$
D
$$1\,mV$$
Answer :
$$0.15\,mV$$
145.
A rectangular loop is present in the magnetic field region of an infinite long wire. Now the loop is being rotated as shown in the figure. Then the induced current in side $$AD$$ will be
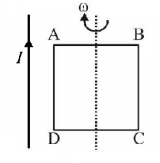
A
along $$DA$$
B
along $$AD$$
C
zero
D
None of these
Answer :
along $$DA$$
146. A rod $$PQ$$ of length $$L$$ moves with a uniform velocity $$v$$ parallel to a long straight wire carrying a current $$i,$$ the end $$P$$ remaining at a distance $$r$$ from the wire. The emf induced across the rod is
A
$$\frac{{{\mu _0}i{v^2}}}{{2\pi }}\ln \left( {\frac{{r + L}}{r}} \right)$$
B
$$\frac{{{\mu _0}{i^2}{v^2}}}{{2\pi }}\ln \left( {\frac{{{r^2} + L}}{r}} \right)$$
C
$$\frac{{{\mu _0}iv}}{{2\pi }}\ln \left( {\frac{{r + L}}{r}} \right)$$
D
$$\frac{{{\mu _0}iv}}{{2\pi }}\ln \left( {\frac{{{r^2} + {L^2}}}{{{L^2}}}} \right)$$
Answer :
$$\frac{{{\mu _0}iv}}{{2\pi }}\ln \left( {\frac{{r + L}}{r}} \right)$$
147.
A sliding wire of length $$0.25\,m$$ and having a resistance of $$0.5\,\Omega $$ moves along conducting guiding rails $$AB$$ and $$CD$$ with a uniform speed of $$4\,m/s.$$ A magnetic field of $$0.5\,T$$ exists normal to the plane of $$ABCD$$ directed into the page. The guides are short-circuited with resistances of 4 and $$2\,\Omega $$ as shown. The current through the sliding wire is :

A
$$0.27\,A$$
B
$$0.37\,A$$
C
$$1.0\,A$$
D
$$0.72\,A$$
Answer :
$$0.27\,A$$
148. A conductor of length $$0.4\,m$$ is moving with a speed of $$7\,m/s$$ perpendicular to a magnetic field of intensity $$0.9\,Wb/{m^2}.$$ The induced emf across the conductor is
A
$$1.26\,V$$
B
$$2.52\,V$$
C
$$5.04\,V$$
D
$$25.2\,V$$
Answer :
$$2.52\,V$$
149. Eddy currents are produced when
A
a metal is kept in varying magnetic field
B
a metal is kept in steady magnetic field
C
a circular coil is placed in a magnetic field
D
current is passed through a circular coil
Answer :
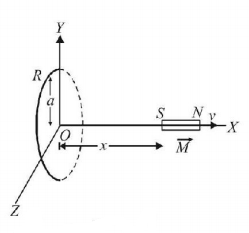
a metal is kept in varying magnetic field
150. An infinitesimally small bar magnet of dipole moment $$\overrightarrow M $$ is pointing and moving with the speed $$v$$ in the $${\hat x}$$- direction. A small closed circular conducting loop of radius $$a$$ and negligible self-inductance lies in the $$y-z$$ plane with its center at $$x =0,$$ and its axis coinciding with the $$x$$-axis. Find the force opposing the motion of the magnet, if the resistance of the loop is $$R.$$ Assume that the distance $$x$$ of the magnet from the center of the loop is much greater than $$a.$$
A
$$\frac{{21}}{4}\frac{{\mu _0^2{M^2}{a^4}v}}{{R{x^8}}}$$
B
$$\frac{{16}}{3}\frac{{{\mu _0}{M^2}{a^2}{v^2}}}{{R{x^3}}}$$
C
$$\frac{3}{{23}}\frac{{{\mu _0}Ma{v^2}}}{{R{x^3}}}$$
D
None of these
Answer :
$$\frac{{21}}{4}\frac{{\mu _0^2{M^2}{a^4}v}}{{R{x^8}}}$$