51. A $$100\,mH$$ coil carries a current of $$1\,A.$$ Energy stored in its magnetic field is
A
$$0.5\,J$$
B
$$1\,A$$
C
$$0.05\,J$$
D
$$0.1\,J$$
Answer :
$$0.05\,J$$
52. In an inductor of self-inductance $$L = 2\,mH,$$ current changes with time according to relation $$i = {t^2}{e^{ - t}}.$$ At what time emf is zero?
A
$$4s$$
B
$$3s$$
C
$$2s$$
D
$$1s$$
Answer :
$$2s$$
53.
In a uniform and constant magnetic field of induction $$B,$$ two long conducting wires $$ab$$ and $$cd$$ are kept parallel to each other at distance $$\ell $$ with their plane perpendicular to $$B.$$ The ends $$a$$ and $$c$$ are connected together by an ideal inductor of inductance $$L.$$ A conducting slider wire $$PQ$$ is imparted a speed $${v_0}$$ at time $$t = 0.$$ The situation is shown in the figure.
At time $$t = \frac{{\pi \sqrt {mL} }}{{4B\ell }},$$ the value of current $$I$$ through the wire $$PQ$$ is (ignore any resistance, electrical as well as mechanical)

A
$$\sqrt {\frac{{mv_0^2}}{L}} $$
B
$$\sqrt {\frac{{mv_0^2}}{{2L}}} $$
C
$$\sqrt {\frac{{mv_0^2}}{{4L}}} $$
D
zero.
Answer :
$$\sqrt {\frac{{mv_0^2}}{{2L}}} $$
54.
A thin semi-circular conducting ring of radius $$R$$ is falling with its plane vertical in horizontal magnetic induction $$\overrightarrow B .$$ At the position $$MNQ$$ the speed of the ring is $$v,$$ and the potential difference developed across the ring is

A
zero
B
$$\frac{{Bv\pi {R^2}}}{2}$$ and $$M$$ is at higher potential
C
$$\pi RBv$$ and $$Q$$ is at higher potential
D
$$2RBv$$ and $$Q$$ is at higher potential
Answer :
$$2RBv$$ and $$Q$$ is at higher potential
55.
The current $$\left( I \right)$$ in the inductance is varying with time according to the plot shown in figure.

Which one of the following is the correct variation of voltage with time in the coil?
A


B
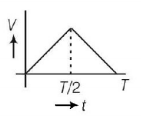

C
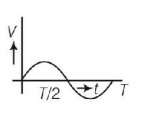

D


Answer :


56. A wire loop is rotated in a magnetic field. The frequency of change of direction of the induced emf is
A
once per revolution
B
twice per revolution
C
four times per revolution
D
six times per revolution
Answer :
twice per revolution
57. A fully charged capacitor $$C$$ with initial charge $${q_0}$$ is connected to a coil of self inductance $$L$$ at $$t = 0.$$ The time at which the energy is stored equally between the electric and the magnetic fields is:
A
$$\frac{\pi }{4}\sqrt {LC} $$
B
$$2\pi \sqrt {LC} $$
C
$$\sqrt {LC} $$
D
$$\pi \sqrt {LC} $$
Answer :
$$\frac{\pi }{4}\sqrt {LC} $$
58. A wire of fixed lengths is wound on a solenoid of length $$\ell $$ and radius $$r.$$ Its self inductance is found to be $$L.$$ Now if same wire is wound on a solenoid of length $$\frac{\ell }{2}$$ and radius $$\frac{r}{2},$$ then the self inductance will be -
A
$$2L$$
B
$$L$$
C
$$4L$$
D
$$8L$$
Answer :
$$2L$$
59. A long solenoid has $$500$$ turns. When a current of $$2$$ ampere is passed through it, the resulting magnetic flux linked with each turn of the solenoid is $$4 \times {10^{ - 3}}Wb.$$ The self- inductance of the solenoid is
A
2.5 henry
B
2.0 henry
C
1.0 henry
D
40 henry
Answer :
1.0 henry
60. Two coaxial solenoids of different radius carry current $$I$$ in the same direction. $$\overrightarrow {{F_1}} $$ be the magnetic force on the inner solenoid due to the outer one and $$\overrightarrow {{F_2}} $$ be the magnetic force on the outer solenoid due to the inner one. Then :
A
$$\overrightarrow {{F_1}} $$ is radially inwards and $$\overrightarrow {{F_2}} = 0$$
B
$$\overrightarrow {{F_1}} $$ is radially outwards and $$\overrightarrow {{F_2}} = 0$$
C
$$\overrightarrow {{F_1}} = \overrightarrow {{F_2}} = 0$$
D
$$\overrightarrow {{F_1}} $$ is radially inwards and $$\overrightarrow {{F_2}} $$ is radially outwards
Answer :
$$\overrightarrow {{F_1}} = \overrightarrow {{F_2}} = 0$$