51. A deutron of kinetic energy $$50\,keV$$ is describing a circular orbit of radius $$0.5\,m$$ in a plane perpendicular to magnetic field $$B.$$ The kinetic energy of the proton that describes a circular orbit of radius $$0.5\,m$$ in the same plane with the same magnetic field $$B$$ is
A
$$25\,keV$$
B
$$50\,keV$$
C
$$200\,keV$$
D
$$100\,keV$$
Answer :
$$100\,keV$$
52. Tesla is the unit of
A
magnetic flux
B
magnetic field
C
magnetic induction
D
magnetic moment
Answer :
magnetic induction
53. A magnetic needle is kept in a non-uniform magnetic field. It experiences
A
neither a force nor a torque
B
a torque but not a force
C
a force but not a torque
D
a force and a torque
Answer :
a force and a torque
54.
A current loop, having two circular arcs joined by two radial
lines is shown in the figure. It carries a current of $$10 A.$$ The magnetic field at point $$O$$ will be close to:

A
$$1.0 \times {10^{ - 7}}T$$
B
$$1.5 \times {10^{ - 7}}T$$
C
$$1.5 \times {10^{ - 5}}T$$
D
$$1.0 \times {10^{ - 5}}T$$
Answer :
$$1.0 \times {10^{ - 5}}T$$
55. Two identical wires $$A$$ and $$B,$$ each of length $$'l',$$ carry the same current $$I.$$ Wire $$A$$ is bent into a circle of radius $$R$$ and wire $$B$$ is bent to form a square of side $$'a’.$$ If $${B_A}$$ and $${B_B}$$ are the values of magnetic field at the centres of the circle and square respectively, then the ratio $$\frac{{{B_A}}}{{{B_B}}}$$ is
A
$$\frac{{{p^2}}}{{16}}$$
B
$$\frac{{{p^2}}}{{8\sqrt 2 }}$$
C
$$\frac{{{p^2}}}{8}$$
D
$$\frac{{{p^2}}}{{16\sqrt 2 }}$$
Answer :
$$\frac{{{p^2}}}{{8\sqrt 2 }}$$
56. A long wire carries a steady current. It is bent into a circle of one turn and the magnetic field at the centre of the coil is $$B.$$ It is then bent into a circular loop of $$n$$ turns. The magnetic field at the centre of the coil will be
A
$$2nB$$
B
$${n^2}B$$
C
$$nB$$
D
$$2{n^2}B$$
Answer :
$${n^2}B$$
57. A current $$I$$ flows through a thin wire shaped as regular polygon of $$n$$ sides which can be inscribed in a circle of radius $$R.$$ The magnetic field induction at the center of polygon due to one side of the polygon is
A
$$\frac{{{\mu _0}I}}{{\pi R}}\left( {\tan \frac{\pi }{n}} \right)$$
B
$$\frac{{{\mu _0}I}}{{4\pi R}}\left( {\tan \frac{\pi }{n}} \right)$$
C
$$\frac{{{\mu _0}I}}{{2\pi R}}\left( {\tan \frac{\pi }{n}} \right)$$
D
$$\frac{{{\mu _0}I}}{{2\pi R}}\left( {\cos \frac{\pi }{n}} \right)$$
Answer :
$$\frac{{{\mu _0}I}}{{2\pi R}}\left( {\tan \frac{\pi }{n}} \right)$$
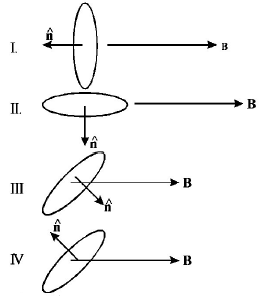
58.
A current carrying loop is placed in a uniform magnetic field in four different orientations, I, II, III & IV arrange them in the decreasing order of Potential Energy
A
$$I>III>II>IV$$
B
$$I>II>III>IV$$
C
$$I>IV>II>III$$
D
$$III>IV>I>II$$
Answer :
$$I>III>II>IV$$
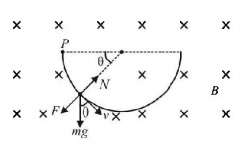
59.
A charged sphere of mass $$m$$ and charge $$- q$$ starts sliding along the surface of a smooth hemispherical bowl, at position $$P.$$ The region has a transverse uniform magnetic field $$B.$$ Normal force by the surface of bowl on the sphere at position $$Q$$ is
A
$$mg\sin \theta + qB\sqrt {2gR\sin \theta } $$
B
$$3\,mg\sin \theta + qB\sqrt {2gR\sin \theta } $$
C
$$mg\sin \theta - qB\sqrt {2gR\sin \theta } $$
D
$$3\,mg\sin \theta - qB\sqrt {2gR\sin \theta } $$
Answer :
$$3\,mg\sin \theta + qB\sqrt {2gR\sin \theta } $$
60.
The magnetic field at $$O$$ due to current in the infinite wire forming a loop as shown in Fig. is

A
$$\frac{{{\mu _0}I}}{{2\pi d}}\left( {\cos {\phi _1} + \cos {\phi _2}} \right)$$
B
$$\frac{{{\mu _0}I2I}}{{4\pi d}}\left( {\tan {\theta _1} + \tan {\theta _2}} \right)$$
C
$$\frac{{{\mu _0}I}}{{4\pi d}}\left( {\sin {\phi _1} + \sin {\phi _2}} \right)$$
D
$$\frac{{{\mu _0}I}}{{4\pi d}}\left( {\cos {\theta _1} + \cos {\theta _2}} \right)$$
Answer :
$$\frac{{{\mu _0}I}}{{2\pi d}}\left( {\cos {\phi _1} + \cos {\phi _2}} \right)$$