51.
The earth’s magnetic field lines resemble that of a dipole at the centre of the earth. If the magnetic moment of this dipole is close to $$8 \times {10^{22}}\,A{m^2},$$ the value of earth’s magnetic field near the equator is close to
(radius of the earth $$ = 6.4 \times {10^6}m$$ )
A
$$0.6\,Gauss$$
B
$$1.2\,Gauss$$
C
$$1.8\,Gauss$$
D
$$0.32\,Gauss$$
Answer :
$$0.6\,Gauss$$
52. Assume that each iron atom has a permanent magnetic moment equal to $$2$$ Bohr magnetons ($$1$$ Bohr magneton $$ = 9.27 \times {10^{ - 24}}A - {m^2}$$ ). The density of atoms in iron is $$8.52 \times {10^{28}}atoms/{m^3}.$$ Find the maximum magnetic moment per unit volume.
A
$$1.5 \times {10^2}A\left| m \right.$$
B
$$1.58 \times {10^6}A\left| m \right.$$
C
$$1.2 \times {10^5}A\left| m \right.$$
D
$$1.3 \times {10^6}A\left| m \right.$$
Answer :
$$1.58 \times {10^6}A\left| m \right.$$
53. The graph between $$\chi $$ and $$\frac{1}{T}$$ for paramagnetic material will be represented by
A


B
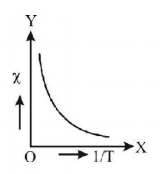

C


D
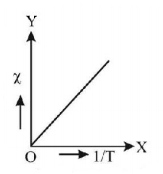

Answer :


54. Two magnets of same size and mass make respectively 10 and 15 oscillations per minute at certain place. The ratio of their magnetic moments is
A
$$4:9$$
B
$$9:4$$
C
$$2:3$$
D
$$3:2$$
Answer :
$$4:9$$
55.
Following figures show the arrangement of bar magnets in different configurations. Each magnet has magnetic dipole moment $$M.$$ Which configuration has highest net magnetic dipole moment?
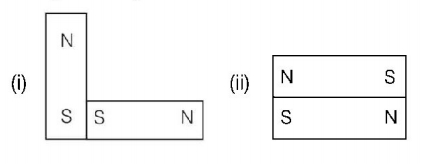
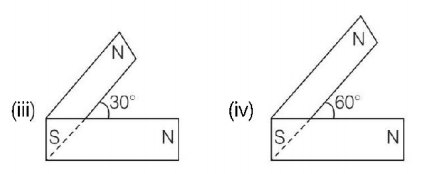
A
(i)
B
(ii)
C
(iii)
D
(iv)
Answer :
(iii)
56. A dip circle is so set that its needle moves freely in the magnetic meridian. In this position, the angle of dip is $${40^ \circ }.$$ Now the dip circle is rotated so that the plane in which the needle moves makes an angle of $${30^ \circ }$$ with the magnetic meridian. In this position, the needle will dip by an angle
A
$${40^ \circ }$$
B
$${30^ \circ }$$
C
more than $${40^ \circ }$$
D
less than $${40^ \circ }$$
Answer :
less than $${40^ \circ }$$
57. A domain in a ferromagnetic substance is in the form of a cube of side length $$1\,\mu m.$$ If it contains $$8 \times {10^{10}}atoms$$ and each atomic dipole has a dipole moment of $$9 \times {10^{ - 24}}A{m^2},$$ then the magnetization of the domain is
A
$$7.2 \times {10^5}\,A{m^{ - 1}}$$
B
$$7.2 \times {10^3}\,A{m^{ - 1}}$$
C
$$7.2 \times {10^9}\,A{m^{ - 1}}$$
D
$$7.2 \times {10^{12}}A{m^{ - 1}}$$
Answer :
$$7.2 \times {10^5}\,A{m^{ - 1}}$$
58. A magnetic dipole is acted upon by two magnetic fields which are inclined to each other at an angle of $${75^ \circ }.$$ One of the fields has a magnitude of $$15\,mT.$$ The dipole attains stable equilibrium at an angle of $${30^ \circ }$$ with this field. The magnitude of the other field (in $$mT$$ ) is close to :
A
1
B
11
C
36
D
1060
Answer :
11
59. At a place, if the earth's horizontal and vertical components of magnetic fields are equal, then the angle of dip will be
A
$${30^ \circ }$$
B
$${90^ \circ }$$
C
$${45^ \circ }$$
D
$${0^ \circ }$$
Answer :
$${45^ \circ }$$
60.
The $$B-H$$ curve (i) and (ii) shown in fig associated with

A
(i) diamagnetic and (ii) paramagnetic substance
B
(i) paramagnetic and (ii) ferromagnetic substance
C
(i) soft iron and (ii) steel
D
(i) steel and (ii) soft iron
Answer :
(i) soft iron and (ii) steel