11.
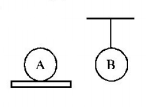
Consider two identical iron spheres , one which lie on a thermally insulating plate, while the other hangs from an insulatory thread. Equal amount of heat is supplied to the two spheres
A
temperature of $$A$$ will be greater than $$B$$
B
temperature of $$B$$ will be greater than $$A$$
C
their temperature will be equal
D
can’t be predicted
Answer :
temperature of $$B$$ will be greater than $$A$$
12.
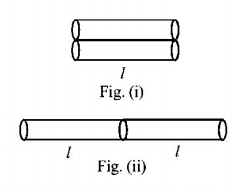
Two rods of same length and transfer a given amount of heat 12 second, when they are joined as shown in figure (i).
But when they are joined as shown in figure (ii), then they will transfer same heat in same conditions in
A
$$24\,s$$
B
$$13\,s$$
C
$$15\,s$$
D
$$48\,s$$
Answer :
$$48\,s$$
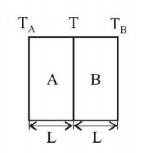
13. A large cylindrical rod of length $$L$$ is made by joining two identical rods of copper and steel of length $$\left( {\frac{L}{2}} \right)$$ each. The rods are completely insulated from the surroundings. If the free end of copper rod is maintained at $${100^ \circ }C$$ and that of steel at $${0^ \circ }C$$ then the temperature of junction is (Thermal conductivity of copper is 9 times that of steel)
A
$${90^ \circ }C$$
B
$${50^ \circ }C$$
C
$${10^ \circ }C$$
D
$${67^ \circ }C$$
Answer :
$${90^ \circ }C$$
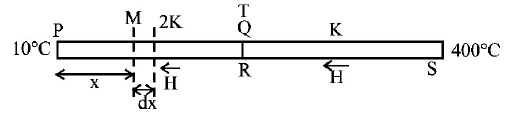
14. The ends $$Q$$ and $$R$$ of two thin wires, $$PQ$$ and $$RS,$$ are soldered (joined) together. Initially each of the wires has a length of $$1\,m$$ at $${10^ \circ }C.$$ Now the end $$P$$ is maintained at $${10^ \circ }C,$$ while the end $$S$$ is heated and maintained at $${400^ \circ }C,$$ The system is thermally insulated from its surroundings. If the thermal conductivity of wire $$PQ$$ is twice that of the wire $$RS$$ and the co-efficient of linear thermal expansion of $$PQ$$ is $$1.2 \times {10^{ - 5}}{K^{ - 1}},$$ the change in length of the wire $$PQ$$ is
A
0.78 $$mm$$
B
0.90 $$mm$$
C
1.56 $$mm$$
D
2.34 $$mm$$
Answer :
0.78 $$mm$$
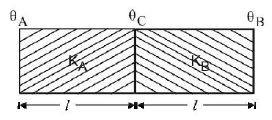
15. A wall has two layers $$A$$ and $$B,$$ each made of different material. Both the layers have the same thickness. The thermal conductivity of the meterial of $$A$$ is twice that of $$B.$$ Under thermal equilibrium, the temperature difference across the wall is $${36^ \circ }C.$$ The temperature difference across the layer $$A$$ is
A
$${6^ \circ }C$$
B
$${12^ \circ }C$$
C
$${18^ \circ }C$$
D
$${24^ \circ }C$$
Answer :
$${12^ \circ }C$$
16. Consider a compound slab consisting of two different materials having equal thicknesses and thermal conductivities $$K$$ and $$2K,$$ respectively. The equivalent thermal conductivity of the slab is
A
$$3K$$
B
$$\frac{4}{3}K$$
C
$$\frac{2}{3}K$$
D
$$\sqrt 2 K$$
Answer :
$$\frac{4}{3}K$$
17.
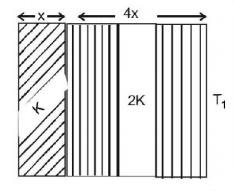
The temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of thermal conductivity $$K$$ and $$2K$$ and thickness $$x$$ and $$4x,$$ respectively, are $${T_2}$$ and $${T_1}\left( {{T_2} > {T_1}} \right).$$ The rate of heat transfer through the slab, in a steady state is $$\left( {\frac{{A\left( {{T_2} - {T_1}} \right)K}}{x}} \right)f,$$ with $$f$$ equal to
A
$$\frac{2}{3}$$
B
$$\frac{1}{2}$$
C
$$1$$
D
$$\frac{1}{3}$$
Answer :
$$\frac{1}{3}$$
18. The two ends of a metal rod are maintained at temperatures $${100^ \circ }C$$ and $${110^ \circ }C.$$ The rate of heat flow in the rod is found to be $$4.0\,J/s.$$ If the ends are maintained at temperatures $${200^ \circ }C$$ and $${210^ \circ }C,$$ the rate of heat flow will be
A
$$16.8\,J/s$$
B
$$8.0\,J/s$$
C
$$4.0\,J/s$$
D
$$44.0\,J/s$$
Answer :
$$4.0\,J/s$$
19. A partition wall has two layers of different materials $$A$$ and $$B$$ in contact with each other. They have the same thickness but the thermal conductivity of layer $$A$$ is twice that of layer $$B.$$ At steady state the temperature difference across the layer $$B$$ is $$50\,K,$$ then the corresponding difference across the layer $$A$$ is
A
$$50\,K$$
B
$$12.5\,K$$
C
$$25\,K$$
D
$$60\,K$$
Answer :
$$25\,K$$
20.
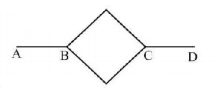
Six identical conducting rods are joined as shown in figure. Points $$A$$ and $$D$$ are maintained at $${200^ \circ }C$$ and $${20^ \circ }C$$ respectively. The temperature of junction $$B$$ will be
A
$${120^ \circ }C$$
B
$${100^ \circ }C$$
C
$${140^ \circ }C$$
D
$${80^ \circ }C$$
Answer :
$${140^ \circ }C$$