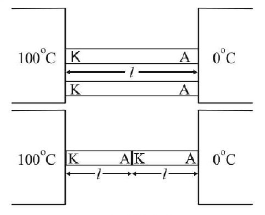
21. Two identical rods are connected between two containers one of them is at $${100^ \circ }C$$ and another is at $${0^ \circ }C.$$ If rods are connected in parallel then the rate of melting of ice is $${q_1}\,gm/sec.$$ If they are connected in series then the rate is $${{q_2}}.$$ The ratio $$\frac{{{q_2}}}{{{q_1}}}$$ is
A
2
B
4
C
$$\frac{1}{2}$$
D
$$\frac{1}{4}$$
Answer :
$$\frac{1}{4}$$
22. Two spheres of different materials one with triple the radius and one-fifth wall thickness of the other are filled with ice. If the time taken for complete melting of ice in the larger sphere is 30 minute and for smaller one is 20 minute, the ratio of thermal conductivities of the materials of larger spheres to that of smaller sphere is
A
$$\frac{1}{8}$$
B
$$\frac{3}{4}$$
C
$$\frac{2}{3}$$
D
$$\frac{1}{2}$$
Answer :
$$\frac{1}{2}$$
23. Two identical bodies are made of a material for which the heat capacity increases with temperature. One of these is at $${100^ \circ }C,$$ while the other one is at $${0^ \circ }C.$$ If the two bodies are brought into contact, then assuming no heat loss, the final common temperature is
A
$${50^ \circ }C$$
B
more than $${50^ \circ }C$$
C
less than $${50^ \circ }C$$ but greater than $${0^ \circ }C$$
D
$${0^ \circ }C$$
Answer :
more than $${50^ \circ }C$$
24.
Two rectangular blocks, having identical dimensions, can be arranged either in configuration - I or in configuration - II as shown in the figure. One of the blocks has thermal conductivity $$k$$ and the other $$2\,k.$$ The temperature difference between the ends along the $$x$$ - axis is the same in both the configurations. It takes $$9\,s$$ to transport a certain amount of heat from the hot end to the cold end in the configuration - I. The time to transport the same amount of heat in the configuration - II is
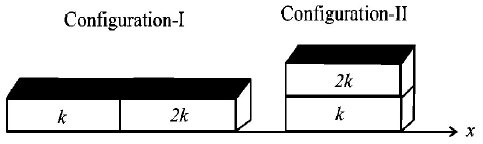
A
$$2.0\,s$$
B
$$4.5\,s$$
C
$$3.0\,s$$
D
$$6.0\,s$$
Answer :
$$2.0\,s$$
25. A cylindrical rod of aluminium is of length $$20\,cms$$ and radius $$2\,cms.$$ The two ends are maintained at temperatures of $${0^ \circ }C$$ and $${50^ \circ }C$$ [the coefficient of thermal conductivity is $$\frac{{0.5\,cal}}{{cm \times \sec { \times ^ \circ }C}}$$ ]. Then the thermal resistance of the rod in $$\frac{{cal}}{{\sec { \times ^ \circ }C}}$$ is
A
318
B
31.8
C
3.18
D
0.318
Answer :
0.318
26.
What is the equivalent thermal conductivity of the rods in figure given below , if the length of each cylinder be $$\ell $$ and area of cylinder having thermal conductivities $${{K_1}}$$ and $${{K_3}}$$ be $$A$$ while that of the middle cylinder haying thermal conductivity $${{K_2}}$$ be $$2A$$ ?
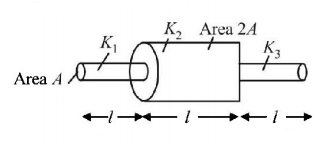
A
$$\frac{5}{{2\left[ {\frac{1}{{{K_1}}} + \frac{1}{{2{K_2}}} + \frac{1}{{{K_3}}}} \right]}}$$
B
$$\frac{1}{{\left[ {\frac{1}{{{K_1}}} + \frac{1}{{2{K_2}}} + \frac{1}{{{K_3}}}} \right]}}$$
C
$$\frac{2}{{5\left[ {\frac{1}{{{K_1}}} + \frac{1}{{2{K_2}}} + \frac{1}{{{K_3}}}} \right]}}$$
D
None of these
Answer :
$$\frac{5}{{2\left[ {\frac{1}{{{K_1}}} + \frac{1}{{2{K_2}}} + \frac{1}{{{K_3}}}} \right]}}$$
27.
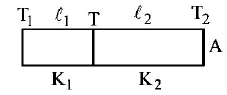
One end of a thermally insulated rod is kept at a temperature $${T_1}$$ and the other at $${T_2}.$$ The rod is composed of two sections of length $${l_1}$$ and $${l_2}$$ and thermal conductivities $${K_1}$$ and $${K_2}$$ respectively. The temperature at the interface of the two section is
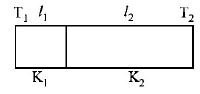
A
$$\frac{{\left( {{K_1}{l _1}{T_1} + {K_2}{l _2}{T_2}} \right)}}{{\left( {{K_1}{l _1} + {K_2}{l _2}} \right)}}$$
B
$$\frac{{\left( {{K_2}{l _2}{T_1} + {K_1}{l _1}{T_2}} \right)}}{{\left( {{K_1}{l _1} + {K_2}{l _2}} \right)}}$$
C
$$\frac{{\left( {{K_2}{l _1}{T_1} + {K_1}{l _2}{T_2}} \right)}}{{\left( {{K_2}{l _1} + {K_1}{l _2}} \right)}}$$
D
$$\frac{{\left( {{K_1}{l _2}{T_1} + {K_2}{l _1}{T_2}} \right)}}{{\left( {{K_1}{l _2} + {K_2}{l _1}} \right)}}$$
Answer :
$$\frac{{\left( {{K_1}{l _2}{T_1} + {K_2}{l _1}{T_2}} \right)}}{{\left( {{K_1}{l _2} + {K_2}{l _1}} \right)}}$$
28.
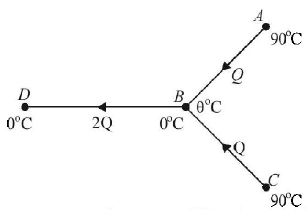
Three rods made of same material and having the same cross-section have been joined as shown in the figure. Each rod is of the same length. The left and right ends are kept at $${0^ \circ }C$$ and $${90^ \circ }C$$ respectively. The temperature of the junction of the three rods will be
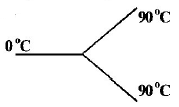
A
$${45^ \circ }C$$
B
$${60^ \circ }C$$
C
$${30^ \circ }C$$
D
$${20^ \circ }C$$
Answer :
$${60^ \circ }C$$
29.
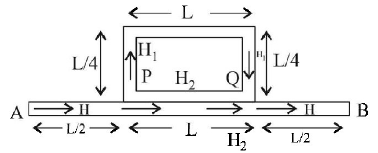
Temperature difference of $$120{\,^ \circ }C$$ is maintained between two ends of a uniform rod $$AB$$ of length $$2\,L.$$ Another bent rod $$PQ,$$ of same cross - section as $$AB$$ and length $$\frac{{3\,L}}{2},$$ is connected across $$AB$$ (See figure). In steady state, temperature difference between $$P$$ and $$Q$$ will be close to :
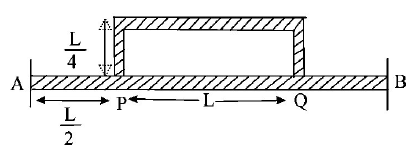
A
$$45{\,^ \circ }C$$
B
$$75{\,^ \circ }C$$
C
$$60{\,^ \circ }C$$
D
$$35{\,^ \circ }C$$
Answer :
$$45{\,^ \circ }C$$
30. The two ends of a metal rod are maintained at temperatures $${100^ \circ }C$$ and $${110^ \circ }C.$$ The rate of heat flow in the rod is found to be $$4.0\,J/s.$$ If the ends are maintained at temperatures $${200^ \circ }C$$ and $${210^ \circ }C,$$ the rate of heat flow will be
A
$$44.0\,J/s$$
B
$$16.8\,J/s$$
C
$$8.0\,J/s$$
D
$$4.0\,J/s$$
Answer :
$$4.0\,J/s$$