141. Which of the following are not electromagnetic waves?
A
cosmic rays
B
gamma rays
C
$$\beta $$ -rays
D
X-rays.
Answer :
$$\beta $$ -rays
142. A proton is bombarded on a stationary Lithium nucleus. As a result of collision two $$\alpha $$-particles are produced. The direction of motion of the $$\alpha $$-particles with the initial direction of motion makes an angle $${\cos ^{ - 1}}\frac{1}{4}.$$ If B.E/Nucleon for $$L{i^7}$$ and $$H{e^4}$$ are $$5.60\,MeV$$ and $$7.06\,MeV$$ respectively, then :
A
Kinetic energy of striking proton is $$17.28\,MeV$$
B
Kinetic energy of striking proton is $$8.64\,MeV$$
C
Kinetic energy of striking proton is $$4.32\,MeV$$
D
Kinetic energy of striking proton is $$2.16\,MeV$$
Answer :
Kinetic energy of striking proton is $$17.28\,MeV$$
143. A nucleus with mass number 220 initially at rest emits an $$\alpha $$ -particle. If the $$Q$$ value of the reaction is $$5.5\,MeV,$$ calculate the kinetic energy of the $$\alpha $$ -particle
A
$$4.4\,MeV$$
B
$$5.4\,MeV$$
C
$$5.6\,MeV$$
D
$$6.5\,MeV$$
Answer :
$$5.4\,MeV$$
144. The activity of a radioactive sample is $${A_1}$$ at time $${t_1}$$ and $${A_2}$$ at time $${t_2}.$$ If $$\tau $$ is average life of sample then the number of nuclei decayed in time $$\left( {{t_2} - {t_1}} \right)$$ is
A
$${A_1}{t_1} - {A_2}{t_2}$$
B
$$\frac{{\left( {{A_1} - {A_2}} \right)}}{2}\tau $$
C
$$\left( {{A_1} - {A_2}} \right)\left( {{t_2} - {t_1}} \right)$$
D
$$\left( {{A_1} - {A_2}} \right)\tau .$$
Answer :
$$\left( {{A_1} - {A_2}} \right)\tau .$$
145. The energy spectrum of $$\beta $$-particles [number $$N\left( E \right)$$ as a function of $$\beta $$-energy $$E$$] emitted from a radioactive source is
A
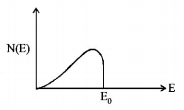

B
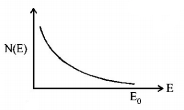

C
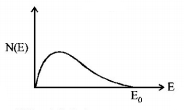

D


Answer :


146. If a star can convert all the He nuclei completely into oxygen nuclei, the energy released per oxygen nuclei is [Mass of He nucleus is $$4.0026\,amu$$ and mass of Oxygen nucleus is $$15.9994\,amu$$ ]
A
$$7.6\,MeV$$
B
$$56.12\,MeV$$
C
$$10.24\,MeV$$
D
$$23.9\,MeV$$
Answer :
$$10.24\,MeV$$
147. A $$^7Li$$ target is bombarded with a proton beam current of $${10^{ - 4}}A$$ for $$1$$ hour to produce $$^7Be$$ of activity $$1.8 \times {10^8}$$ disintegrations per second. Assuming that one $$^7Be$$ radioactive nucleus is produced by bombarding $$1000$$ protons, determine its half life.
A
$$8.6 \times {10^6}s$$
B
$$4.2 \times {10^5}s$$
C
$$3.1 \times {10^5}s$$
D
$$1.1 \times {10^6}s$$
Answer :
$$8.6 \times {10^6}s$$
148. Which of the following cannot be emitted by radioactive substances during their decay ?
A
Protons
B
Neutrinoes
C
Helium nuclei
D
Electrons
Answer :
Protons
149. The intensity of gamma radiation from a given source is $$I.$$ On passing through $$36\,mm$$ of lead, it is reduced to $$\frac{I}{8}.$$ The thickness of lead which will reduce the intensity to $$\frac{I}{2}$$ will be
A
$$9mm$$
B
$$6mm$$
C
$$12mm$$
D
$$18mm$$
Answer :
$$12mm$$
150. $$_{87}^{221}Ra$$ is a radioactive substance having half life of 4 days. Find the probability that a nucleus undergoes decay after two half lives
A
1
B
$$\frac{1}{2}$$
C
$$\frac{3}{4}$$
D
$$\frac{1}{4}$$
Answer :
$$\frac{3}{4}$$