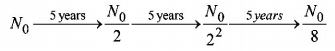41. A nucleus disintegrated into two nuclear parts which have their velocities in the ratio of 2 : 1. The ratio of their nuclear sizes will be
A
$${3^{\frac{1}{2}}}:1$$
B
$$1:{2^{\frac{1}{3}}}$$
C
$${2^{\frac{1}{3}}}:1$$
D
$$1:{3^{\frac{1}{2}}}$$
Answer :
$$1:{2^{\frac{1}{3}}}$$
42.
The masses of neutron and proton are $$1.0087\,a.m.u.$$ and $$1.0073\,a.m.u.$$ respectively. If the neutrons and protons combine to form a helium nucleus (alpha particles) of mass $$4.0015\,a.m.u$$ the binding energy of the helium nucleus will be
$$\left( {1\,a.m.u = 931\,MeV} \right)$$
A
$$28.4\,MeV$$
B
$$20.8\,MeV$$
C
$$27.3\,MeV$$
D
$$14.2\,MeV$$
Answer :
$$28.4\,MeV$$
43. A radioactive nucleus (initial mass number $$A$$ and atomic number $$Z$$ emits 3 $$\alpha $$ - particles and 2 positrons. The ratio of number of neutrons to that of protons in the final nucleus will be
A
$$\frac{{A - Z - 8}}{{Z - 4}}$$
B
$$\frac{{A - Z - 4}}{{Z - 8}}$$
C
$$\frac{{A - Z - 12}}{{Z - 4}}$$
D
$$\frac{{A - Z - 4}}{{Z - 2}}$$
Answer :
$$\frac{{A - Z - 4}}{{Z - 8}}$$
44.
The element curium $$_{96}C{m^{248}}$$ has a mean life of $${10^{13}}s.$$ Its primary decay modes are spontaneous fission and $$\alpha $$-decay, the former with a probability of $$8\% $$ and the later with a probability of $$92\% .$$ Each fission releases $$200\,MeV$$ of energy. The masses involved in $$\alpha $$ decay are as follows:
$$_{96}C{m^{248}} = 248.072220\,u,{\,_{94}}P{u^{244}} = 244.064100\,u$$ and $$_2H{e^4} = 4.002603\,u$$
Calculate the power output from a sample of $${10^{20}}Cm$$ atoms.
$$\left( {1u = 931\,MeV/{c^2}} \right).$$
A
$$1.6 \times {10^{ - 5}}W$$
B
$$2.6 \times {10^{ - 3}}W$$
C
$$3.3 \times {10^{ - 5}}W$$
D
$$5.1 \times {10^{ - 3}}W$$
Answer :
$$3.3 \times {10^{ - 5}}W$$
45. If $${N_0}$$ is the original mass of the substance of half-life period $${t_{\frac{1}{2}}} = 5$$ years, then the amount of substance left after 15 years is
A
$$\frac{{{N_0}}}{8}$$
B
$$\frac{{{N_0}}}{{16}}$$
C
$$\frac{{{N_0}}}{2}$$
D
$$\frac{{{N_0}}}{4}$$
Answer :
$$\frac{{{N_0}}}{8}$$
46. One gram of a radioactive sample of half-life $$10\,\min$$ is sealed in a capsule at time $$t= 0.$$ Amount of sample decayed upto $$5\,\min$$ is
A
$$0.293\,g$$
B
$$0.5\,g$$
C
$$0.25\,g$$
D
$$0.707\,g$$
Answer :
$$0.293\,g$$
47. A sample of radioactive elements contains $$4 \times {10^{10}}$$ active nuclei. If half-life of element is 10 days, then the number of decayed nuclei after 30 days is
A
$$0.5 \times {10^{10}}$$
B
$$2 \times {10^{10}}$$
C
$$3.5 \times {10^{10}}$$
D
$$1 \times {10^{10}}$$
Answer :
$$3.5 \times {10^{10}}$$
48. A nucleus $$_Z^AX$$ has mass represented by $$m\left( {A,Z} \right).$$ lf $${m_p}$$ and $${m_n}$$ denote the mass of proton and neutron respectively and $$BE$$ the binding energy (in $$MeV$$ ), then
A
$$BE = \left[ {m\left( {A,Z} \right) - Z{m_p} - \left( {A - Z} \right){m_n}} \right]{c^2}$$
B
$$BE = \left[ {Z{m_p} + \left( {A - Z} \right){m_n} - m\left( {A,Z} \right)} \right]{c^2}$$
C
$$BE = \left[ {Z{m_p} + A{m_n} - m\left( {A,Z} \right)} \right]{c^2}$$
D
$$BE = m\left( {A,Z} \right) - Z{m_p} - \left( {A - Z} \right){m_n}$$
Answer :
$$BE = \left[ {Z{m_p} + \left( {A - Z} \right){m_n} - m\left( {A,Z} \right)} \right]{c^2}$$
49. The activity of a radioactive sample is measured as $${N_0}$$ counts per minute at $$t= 0$$ and $$\frac{{{N_0}}}{e}$$ counts per minute at $$t= 5$$ minutes. The time (in minutes) at which the activity reduces to half its value is
A
$$\frac{{{{\log }_e}2}}{5}$$
B
$$\frac{5}{{{{\log }_e}2}}$$
C
$$5{\log _{10}}2$$
D
$$5{\log _e}2$$
Answer :
$$5{\log _e}2$$
50. At a specific instant emission of radioactive compound is deflected in a magnetic field. The compound can emit
A
electrons
B
protons
C
$$H{e^{2 + }}$$
D
neutrons
Answer :
electrons