141.
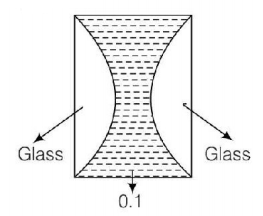
A ray of light is incident on a thick slab of glass (thickness $$t$$) as shown below. The emergent ray is parallel to the incident ray but displaced sideways by a distance $$d.$$ If the angles are small then $$d$$ is :

A
$$t\left( {1 - \frac{i}{r}} \right)$$
B
$$r\,t\left( {1 - \frac{i}{r}} \right)$$
C
$$i\,t\left( {1 - \frac{r}{i}} \right)$$
D
$$t\left( {1 - \frac{r}{i}} \right)$$
Answer :
$$i\,t\left( {1 - \frac{r}{i}} \right)$$
142. A ray of light travelling in a transparent medium of refractive index $$\mu $$ falls, on a surface separating the medium from air at an angle of incidence of $${45^ \circ }.$$ For which of the following value of $$\mu $$ the ray can undergo total internal reflection?
A
$$\mu = 1.33$$
B
$$\mu = 1.40$$
C
$$\mu = 1.50$$
D
$$\mu = 1.25$$
Answer :
$$\mu = 1.50$$
143. A point source of light is placed $$4\,m$$ below the surface of water of refractive index $$\frac{5}{3}.$$ The minimum diameter of a disc, which should be placed over the source, on the surface of water to cut off all light coming out of water is
A
infinite
B
$$6\,m$$
C
$$4\,m$$
D
$$3\,m$$
Answer :
$$6\,m$$
144. In a double slit experiment, the two slits are $$1\,mm$$ apart and the screen is placed $$1\,m$$ away. A monochromatic light of wavelength $$500\,nm$$ is used. What will be the width of each slit for obtaining ten maxima of double slit within the central maxima of single slit pattern?
A
$$0.2\,mm$$
B
$$0.1\,mm$$
C
$$0.5\,mm$$
D
$$0.02\,mm$$
Answer :
$$0.2\,mm$$
145.
The following data are given for a crown glass prism ;
refractive index for violet light $${n_v} = 1.521$$
refractive index for red light $${n_r} = 1.510$$
refractive index for yellow light $${n_y} = 1.515$$
Then the dispersive power of a parallel glass slab made of the same material is
A
0.01
B
0.03
C
0
D
0.02
Answer :
0.02
146. The width of man's face is $$10\,cm.$$ The distance between the eyes of the man is $$4\,cm.$$ Then the minimum width of plane mirror to see his full face, is
A
$$5\,cm$$
B
$$4\,cm$$
C
$$3\,cm$$
D
$$10\,cm$$
Answer :
$$3\,cm$$
147. Assuming human pupil to have a radius of $$0.25\,cm$$ and a comfortable viewing distance of $$25\,cm,$$ the minimum separation between two objects that human eye can resolve at $$500\,nm$$ wavelength is:
A
$$100\,\mu m$$
B
$$300\,\mu m$$
C
$$1\,\mu m$$
D
$$30\,\mu m$$
Answer :
$$30\,\mu m$$
148. A convex lens is dipped in a liquid whose refractive index is equal to the refractive index of the lens. Then its focal length will
A
become small, but non-zero
B
remain unchanged
C
become zero
D
become infinite
Answer :
become infinite
149. Two identical thin plano-convex glass lenses (refractive index 1.5) each having radius of curvature of $$20\,cm$$ are placed with their convex surfaces in contact at the centre. The intervening space is filled with oil of refractive index 1.7. The focal length of the combination is
A
$$ - 20\,cm$$
B
$$ - 25\,cm$$
C
$$ - 50\,cm$$
D
$$50\,cm$$
Answer :
$$ - 50\,cm$$
150.
A ray of light from a denser medium strike a rarer medium at an angle of incidence $$i$$ (see Fig). The reflected and retracted rays make an angle of $${{{90}^ \circ }}$$ with each other. The angles of reflection and refraction are $$r$$ and $$r’$$ The critical angle is

A
$${\sin ^{ - 1}}\left( {\tan r} \right)$$
B
$${\sin ^{ - 1}}\left( {\tan i} \right)$$
C
$${\sin ^{ - 1}}\left( {\tan r'} \right)$$
D
$${\tan ^{ - 1}}\left( {\sin i} \right)$$
Answer :
$${\sin ^{ - 1}}\left( {\tan r} \right)$$