11. The focal lengths of the objective and the eye piece of a compound microscope are $$2.0\,cm$$ and $$3.0\,cm,$$ respectively. The distance between the objective and the eye piece is $$15.0\,cm.$$ The final image formed by the eye piece is at infinity. The two lenses are thin. The distance in $$cm$$ of the object and the image produced by the objective, measured from the objective lens, are respectively
A
2.4 and 12.0
B
2.4 and 15.0
C
2.0 and 12.0
D
2.0 and 3.0
Answer :
2.4 and 12.0
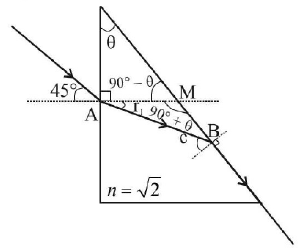
12.
A parallel beam of light is incident from air at an angle $$\alpha $$ on the side $$PQ$$ of a right angled triangular prism of refractive index $$n = \sqrt 2 .$$ Light undergoes total internal reflection in the prism at the face $$PR$$ when $$\alpha $$ has a minimum value of 45°. The angle $$\,\theta $$ of the prism is

A
15°
B
22.5°
C
30°
D
45°
Answer :
15°
13. Young’s double slit experiment is first performed in air and then in a medium other than air. It is found that 8th bright fringe in the medium lies where 5th dark fringe lies in air. The refractive index of the medium is nearly
A
1.25
B
1.59
C
1.69
D
1.78
Answer :
1.78
14. Which of the following phenomenon is not common to sound and light waves ?
A
Interference
B
Diffraction
C
Coherence
D
Polarisation
Answer :
Polarisation
15.
A point object is located at a distance $$15\,cm.$$ from the pole of a concave mirror of focal length $$10\,cm$$ on its principal axis is moving with a velocity $$\left( {8\hat i + 11\hat j} \right)cm/s$$ and velocity of mirror is $$\left( {4\hat i + 2\hat j} \right)cm/s$$ as shown. If $${\vec v}$$ is the velocity of image. Then find the value of $$\left| {\vec v} \right|$$ in $$\left( {cm/s} \right).$$

A
20
B
30
C
10
D
40
Answer :
20
16. A point object is placed at the centre of a glass sphere of radius $$6\,cm$$ and refractive index 1.5. The distance of virtual image from the surface is
A
$$6\,cm$$
B
$$4\,cm$$
C
$$12\,cm$$
D
$$9\,cm$$
Answer :
$$6\,cm$$
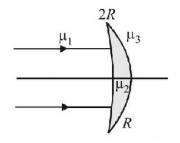
17.
Figure shows a concavo-convex lens $${\mu _2}.$$ What is the condition on the reflective indices so that the lens is diverging?
A
$$2{\mu _3} < {\mu _1} + {\mu _2}$$
B
$$2{\mu _3} > {\mu _1} + {\mu _2}$$
C
$${\mu _3} > 2\left( {{\mu _1} - {\mu _2}} \right)$$
D
None of these
Answer :
$$2{\mu _3} > {\mu _1} + {\mu _2}$$
18. For a normal eye, the cornea of eye provides a converging power of $$40\,D$$ and the least converging power of the eye lens behind the cornea is $$20\,D.$$ Using this information, the distance between the retina and the cornea, eye lens can be estimated to be
A
$$5\,cm$$
B
$$2.5\,cm$$
C
$$1.67\,cm$$
D
$$1.5\,cm$$
Answer :
$$1.67\,cm$$
19. The hypermetropia is a
A
short-sight defect
B
long-sight defect
C
bad vision due to old age
D
None of the above
Answer :
long-sight defect
20.
In a vessel, as shown in Fig. point $$P$$ is just visible when no liquid is filled in vessel through a telescope in the air. When liquid is filled in the vessel completely, point $$Q$$ is visible without moving the vessel or telescope. Find the refractive index of the liquid.

A
$$\frac{{\sqrt {14} }}{3}$$
B
$$\frac{{\sqrt {85} }}{5}$$
C
$$\sqrt 2 $$
D
$$\sqrt 3 $$
Answer :
$$\frac{{\sqrt {85} }}{5}$$