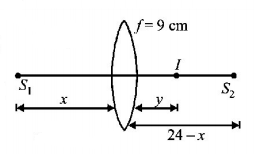
201. Two point source $${S_1}$$ and $${S_2}$$ are $$24\,cm$$ apart. Where should a convex lens of focal length $$9\,cm$$ be placed in between them so that the images of both sources are formed at the same place?
A
$$6\,cm$$ from $${S_1}$$
B
$$15\,cm$$ from $${S_1}$$
C
$$10\,cm$$ from $${S_1}$$
D
$$12\,cm$$ from $${S_1}$$
Answer :
$$6\,cm$$ from $${S_1}$$
202. Transmission of light in optical fibre is due to
A
scattering
B
diffraction
C
polarisation
D
multiple total internal reflections
Answer :
multiple total internal reflections
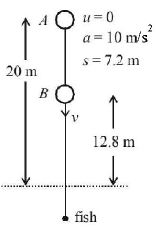
203. A ball is dropped from a height of $$20\,m$$ above the surface of water in a lake. The refractive index of water is $$4.3.$$ A fish inside the lake, in the line of fall of the ball, is looking at the ball. At an instant, when the ball is $$12.8\,m$$ above the water surface, the fish sees the speed of ball as [Take $$g = 10\,m/{s^2}.$$ ]
A
$$9\,m/s$$
B
$$12\,m/s$$
C
$$16\,m/s$$
D
$$21.33\,m/s$$
Answer :
$$16\,m/s$$
204. A green light is incident from the water to the air-water interface at the critical angle $$\left( \theta \right).$$ Select the correct statement.
A
The entire spectrum of visible light will come out of the water at an angle of 90° to the normal.
B
The spectrum of visible light whose frequency is less than that of green light will come out to the air medium.
C
The spectrum of visible light whose frequency is more than that of green light will come out to the air medium.
D
The entire spectrum of visible light will come out of the water at various angles to the normal.
Answer :
The spectrum of visible light whose frequency is less than that of green light will come out to the air medium.
205. Angle of deviation $$\left( \delta \right)$$ by a prism (refractive index $$ = \mu ,$$ and supposing the angle of prism $$A$$ to be small) can be given by
A
$$\delta = \left( {\mu - 1} \right)A$$
B
$$\delta = \left( {\mu + 1} \right)A$$
C
$$\delta = \frac{{\sin \frac{{A + \delta }}{2}}}{{\sin \frac{A}{2}}}$$
D
$$\delta = \frac{{\mu - 1}}{{\mu + 1}}A$$
Answer :
$$\delta = \left( {\mu - 1} \right)A$$
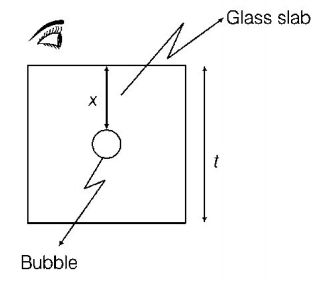
206. An air bubble in a glass slab with refractive index $$1.5$$ (near normal incidence) is $$5\,cm$$ deep when viewed from one surface and $$3\,cm$$ deep when viewed from the opposite face. The thickness (in $$cm$$ ) of the slab is
A
8
B
10
C
12
D
16
Answer :
12
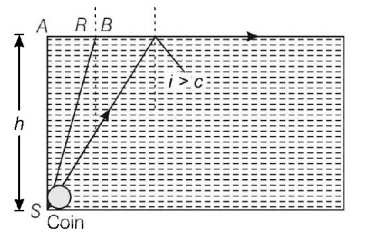
207.
A small coin is resting on the bottom of a beaker filled with a liquid. A ray of light from the coin travels upto the surface of the liquid and moves along its surface
(see figure).
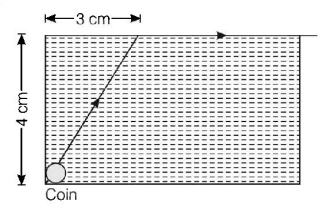
How fast is the light travelling in the liquid?
A
$$1.8 \times {10^8}m/s$$
B
$$2.4 \times {10^8}m/s$$
C
$$3.0 \times {10^8}m/s$$
D
$$1.2 \times {10^4}m/s$$
Answer :
$$1.8 \times {10^8}m/s$$
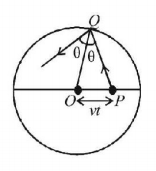
208. A point light source is moving with a constant velocity $$v$$ inside a transparent thin spherical shell of radius $$R,$$ which is filled with a transparent liquid. If at $$t = 0$$ light source is at the centre of the sphere, then at what time a thin dark ring will be visible for an observer outside the sphere. The refractive index of liquid with respect to that of shell is $$\sqrt 2 .$$
A
$$\frac{R}{{\sqrt 2 V}}$$
B
$$\frac{R}{{2V}}$$
C
$$\frac{R}{{3V}}$$
D
$$\frac{R}{{\sqrt 3 V}}$$
Answer :
$$\frac{R}{{\sqrt 2 V}}$$
209. A linear aperture whose width is $$0.02\,cm$$ is placed immediately in front of a lens of focal length $$60\,cm.$$ The aperture is illuminated normally by a parallel beam of wavelength $$5 \times {10^{ - 5}}cm.$$ The distance of the first dark band of the diffraction pattern from the centre of the screen is
A
$$0.10\,cm$$
B
$$0.25\,cm$$
C
$$0.20\,cm$$
D
$$0.15\,cm$$
Answer :
$$0.15\,cm$$
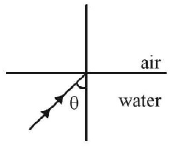
210.
For the given incident ray as shown in figure, the condition of total internal reflection of the ray will be satisfied if the refractive index of block will be
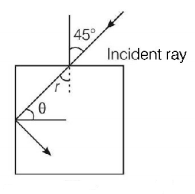
A
$$\frac{{\sqrt 3 + 1}}{2}$$
B
$$\frac{{\sqrt 2 + 1}}{2}$$
C
$$\sqrt {\frac{3}{2}} $$
D
$$\sqrt {\frac{7}{6}} $$
Answer :
$$\sqrt {\frac{3}{2}} $$