41.
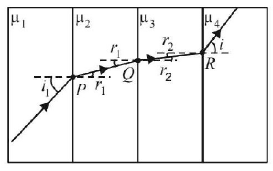
Focal length of the plano-convex lens is $$15\,cm.$$ A small object is placed at $$A$$ as shown in the figure. The plane surface is silvered. The image will form at
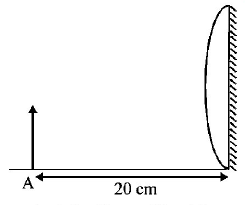
A
$$60\,cm$$ to the left of lens
B
$$12\,cm$$ to the left of lens
C
$$60\,cm$$ to the right of lens
D
$$30\,cm$$ to the left of lens
Answer :
$$12\,cm$$ to the left of lens
42. A lens is placed between a source of light and a wall. It forms images of area $${A_1}$$ and $${A_2}$$ on the wall, for its two different positions, the area of the source of light is
A
$$\sqrt {{A_1}{A_2}} $$
B
$$\frac{{{A_1} + {A_2}}}{2}$$
C
$$\frac{{{A_1} - {A_2}}}{2}$$
D
$$\frac{1}{{{A_1}}} + \frac{1}{{{A_2}}}$$
Answer :
$$\sqrt {{A_1}{A_2}} $$
43. An achromatic combination of lenses is formed by joining
A
2 convex lenses
B
2 concave lenses
C
1 convex, 1 concave lens
D
1 convex and 1 plane mirror
Answer :
1 convex, 1 concave lens
44. Which of the following is not due to total internal reflection?
A
Difference between apparent and real depth of a pond
B
Mirage on hot summer days
C
Brilliance of diamond
D
Working of optical fibre
Answer :
Difference between apparent and real depth of a pond
45.
A ray of light passes through four transparent media with refractive indices $${\mu _1},{\mu _2},{\mu _3}$$ and $${\mu _4}$$ as shown in the figure. The surfaces of all media are parallel. If the emergent ray $$CD$$ is parallel to the incident ray $$AB,$$ we must have
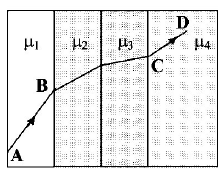
A
$${\mu _1} = {\mu _2}$$
B
$${\mu _2} = {\mu _3}$$
C
$${\mu _3} = {\mu _4}$$
D
$${\mu _4} = {\mu _1}$$
Answer :
$${\mu _4} = {\mu _1}$$
46.
A ray of light is incident at the glass-water interface at an angle $$i,$$ it emerges finally parallel to the surface of water, then the value of $${\mu _g}$$ would be
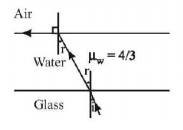
A
$$\left( {\frac{4}{3}} \right)\sin i$$
B
$$\frac{1}{{\sin i}}$$
C
$${\frac{4}{3}}$$
D
$$1$$
Answer :
$$\frac{1}{{\sin i}}$$
47. A short linear object of length $$\ell $$ lies along the axis of a concave mirror of focal length $$f$$ at a distance $$u$$ from the pole of the mirror. The size of the image is approximately equal to
A
$$\ell {\left( {\frac{{u - f}}{f}} \right)^{\frac{1}{2}}}$$
B
$$\ell {\left( {\frac{{u - f}}{f}} \right)^2}$$
C
$$\ell {\left( {\frac{f}{{u - f}}} \right)^{\frac{1}{2}}}$$
D
$$\ell {\left( {\frac{f}{{u - f}}} \right)^2}$$
Answer :
$$\ell {\left( {\frac{f}{{u - f}}} \right)^2}$$
48. The intensity at the maximum in a Young’s double slit experiment is $${I_0}.$$ Distance between two slits is $$d = 5\lambda ,$$ where $$\lambda $$ is the wavelength of light used in the experiment. What will be the intensity infront of one of the slits on the screen placed at a distance $$D = 10\,d$$ ?
A
$$\frac{{{I_0}}}{4}$$
B
$$\frac{3}{4}{I_0}$$
C
$$\frac{{{I_0}}}{2}$$
D
$${I_0}$$
Answer :
$$\frac{{{I_0}}}{2}$$
49. If two mirrors are kept at 60° to each other, then the number of images formed by them is
A
5
B
6
C
7
D
8
Answer :
5
50. The focal lengths of a converging lens measured for violet, green and red colours are $${f_V},{f_G},{f_R}$$ respectively. We will find
A
$${f_G} > {f_R}$$
B
$${f_V} < {f_R}$$
C
$${f_V} > {f_R}$$
D
$${f_V} = {f_R}$$
Answer :
$${f_V} < {f_R}$$