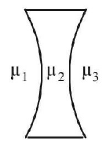
51. A plano-convex lens fits exactly into a plano-concave lens. Their plane surfaces are parallel to each other. If lenses are made of different materials of refractive indices $${\mu _1}$$ and $${\mu _2}$$ and $$R$$ is the radius of curvature of the curved surface of the lenses, then the focal length of the combination is
A
$$\frac{R}{{2\left( {{\mu _1} + {\mu _2}} \right)}}$$
B
$$\frac{R}{{2\left( {{\mu _1} - {\mu _2}} \right)}}$$
C
$$\frac{R}{{\left( {{\mu _1} - {\mu _2}} \right)}}$$
D
$$\frac{{2R}}{{\left( {{\mu _2} - {\mu _1}} \right)}}$$
Answer :
$$\frac{R}{{\left( {{\mu _1} - {\mu _2}} \right)}}$$
52. A planoconvex lens is made of a material of refractive index $$\mu = 1.5.$$ The radius of curvature of curved surface of the lens is $$20\,cm.$$ If its plane surface is silvered, the focal length of the silvered lens will be
A
$$10\,cm$$
B
$$20\,cm$$
C
$$40\,cm$$
D
$$80\,cm$$
Answer :
$$20\,cm$$
53. A hollow double concave lens is made of very thin transparent material. It can be filled with air or either of two liquids $${L_1}$$ or $${L_2}$$ having refractive indices $${\mu _1}$$ and $${\mu _2}$$ respectively $$\left( {{\mu _2} > {\mu _1} > 1} \right).$$ The lens will diverge a parallel beam of light if it is filled with
A
air and placed in air
B
air and immersed in $${L_1}$$
C
$${L_1}$$ and immersed in $${L_2}$$
D
$${L_2}$$ and immersed in $${L_1}$$
Answer :
$${L_2}$$ and immersed in $${L_1}$$
54. A convex lens of focal length $$80\,cm$$ and a concave lens of focal length $$50\,cm$$ are combined together. What will be their resulting power ?
A
$$ + 6.5\,D$$
B
$$ - 6.5\,D$$
C
$$ + 7.5\,D$$
D
$$ - 0.75\,D$$
Answer :
$$ - 0.75\,D$$
55. A scuba diver in an empty swimming pool uses a magnifier $$\left( {n = 1.25} \right)$$ to enlarge the print on a plastic instruction sheet. If the pool is filled with water $$\left( {n = 1.33} \right)$$ what happens to the magnification of the print ?
A
It increases and is greater than one.
B
It stays the same.
C
It decreases, but is still greater than one.
D
It decreases and is less than one
Answer :
It decreases and is less than one
56.
A glass prism of refractive index 1.5 is immersed in water (refractive index $$\frac{4}{3}$$ ). A light beam incident normally on the face $$AB$$ is totally reflected to reach on the face $$BC$$ if

A
$$\sin \theta \geqslant \frac{8}{9}$$
B
$$\frac{2}{3} < \sin \theta < \frac{8}{9}$$
C
$$\sin \theta \leqslant \frac{2}{3}$$
D
None of these
Answer :
$$\sin \theta \geqslant \frac{8}{9}$$
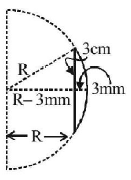
57. Diameter of a plano-convex lens is $$6\,cm$$ and thickness at the centre is $$3\,mm.$$ If speed of light in material of lens is $$2 \times {10^8}m/s,$$ the focal length of the lens is
A
$$15\,cm$$
B
$$20\,cm$$
C
$$30\,cm$$
D
$$10\,cm$$
Answer :
$$30\,cm$$
58. Which one of the following spherical lenses does not exhibit dispersion? The radii of curvature of the surfaces of the lenses are as given in the diagrams.
A
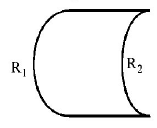

B
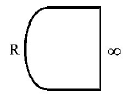

C
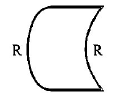
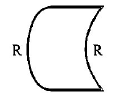
D
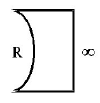

Answer :
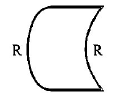
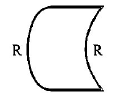
59. The Young’s modulus of steel is twice that of brass. Two wires of same length and of same area of cross-section, one of steel and another of brass are suspended from the same roof. It we want the lower ends of the wires to be at the same level, then the weight added to the steel and brass wires must be in the ratio of
A
$$1:2$$
B
$$2:1$$
C
$$4:1$$
D
$$1:1$$
Answer :
$$2:1$$
60. A concave lens of glass, refractive index 1.5 has both surfaces of same radius of curvature $$R.$$ On immersion in a medium of refractive index 1.75, it will behave as a
A
convergent lens of focal length $$3.5\,R$$
B
convergent lens of focal length $$3.0\,R$$
C
divergent lens of focal length $$3.5\,R$$
D
divergent lens of focal length $$3.0\,R$$
Answer :
convergent lens of focal length $$3.5\,R$$