61. Time taken by sunlight to pass through a window of thickness $$4\,mm$$ whose refractive index is $$\frac{3}{2},$$ is
A
$$2 \times {10^{ - 4}}s$$
B
$$2 \times {10^8}s$$
C
$$2 \times {10^{ - 11}}s$$
D
$$2 \times {10^{11}}s$$
Answer :
$$2 \times {10^{ - 11}}s$$
62.
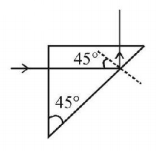
A triangular prism of glass is inside water. A ray, incident normally, on one of the faces, is totally reflected from face $$BC.$$ Then the minimum refractive index of glass is -

A
$$\frac{{\sqrt 3 }}{2}$$
B
$$\frac{5}{3}$$
C
$$\frac{{2\sqrt 2 }}{5}$$
D
$$\frac{{4\sqrt 2 }}{3}$$
Answer :
$$\frac{{4\sqrt 2 }}{3}$$
63. Colours of thin soap bubbles are due to
A
refraction
B
dispersion
C
interference
D
diffraction
Answer :
interference
64. The magnifying power of a telescope is 9. When it is adjusted for parallel rays the distance between the objective and eyepiece is $$20\,cm.$$ The focal length of lenses are
A
$$10\,cm,\,10\,cm$$
B
$$15\,cm,\,5\,cm$$
C
$$18\,cm,\,2\,cm$$
D
$$11\,cm,\,9\,cm$$
Answer :
$$18\,cm,\,2\,cm$$
65. A body is located on a wall. Its image of equal size is to be obtained on a parallel wall with the help of a convex lens. The lens is placed at a distance $$d$$ ahead of second wall, then the required focal length will be
A
only $$\frac{d}{4}$$
B
only $$\frac{d}{2}$$
C
more than $$\frac{d}{4}$$ but less than $$\frac{d}{2}$$
D
less than $$\frac{d}{4}$$
Answer :
only $$\frac{d}{2}$$
66. The focal lengths of objective lens and eye lens of a Galilean telescope are respectively $$30\,cm$$ and $$3.0\,cm.$$ telescope produces virtual, erect image of an object situated far away from it at least distance of distinct vision from the eye lens. In this condition, the magnifying power of the Galilean telescope should be:
A
$$+ 11.2$$
B
$$- 11.2$$
C
$$- 8.8$$
D
$$+ 8.8$$
Answer :
$$+ 8.8$$
67. A man is $$6\,ft$$ tall. In order to see his entire image, he requires a plane mirror of minimum length equal to
A
$$6\,ft$$
B
$$12\,ft$$
C
$$2\,ft$$
D
$$3\,ft$$
Answer :
$$3\,ft$$
68. A convex lens is put $$10\,cm$$ from a light source and it makes a sharp image on a screen, kept $$10\,cm$$ from the lens. Now a glass block (refractive index 1.5) of $$1.5\,cm$$ thickness is placed in contact with the light source. To get the sharp image again, the screem is shifted by a distance $$d.$$ Then $$d$$ is:
A
$$1.1\,cm$$ away from the lens
B
0
C
$$0.55\,cm$$ towards the lens
D
$$0.55\,cm$$ away from the lens
Answer :
$$0.55\,cm$$ away from the lens
69.
A glass sphere, refractive index 1.5 and radius $$10\,cm,$$ has a spherical cavity of radius $$5\,cm$$ concentric with it. A narrow beam of parallel light is directed into the sphere. Find the final image and its nature.

A
$$25\,cm$$ left of $${S_4},$$ virtual
B
$$25\,cm$$ right of $${S_4},$$ real
C
$$15\,cm$$ left of $${S_4},$$ virtual
D
$$20\,cm$$ right of $${S_4},$$ virtual
Answer :
$$25\,cm$$ left of $${S_4},$$ virtual
70. In the Young’s double-slit experiment, the intensity of light at a point on the screen (where the path difference is $$\lambda $$) is $$K,$$ ($$\lambda $$ being the wavelength of light used). The intensity at a point where the path difference is $$\frac{\lambda }{4},$$ will be
A
$$K$$
B
$$\frac{K}{4}$$
C
$$\frac{K}{2}$$
D
zero
Answer :
$$\frac{K}{2}$$