71. Spherical aberration in a thin lens can be reduced by
A
using a monochromatic light
B
using a doublet combination
C
using a circular annular mark over the lens
D
increasing the size of the lens.
Answer :
using a circular annular mark over the lens
72. A concave mirror for face viewing has focal length of $$0.4\,m.$$ The distance at which you hold the mirror from your face in order to see your image upright with a magnification of 5 is:
A
$$0.24\,m$$
B
$$1.60\,m$$
C
$$0.32\,m$$
D
$$0.16\,m$$
Answer :
$$0.32\,m$$
73. Two mirrors, one concave and the other convex, are placed $$60\,cm$$ apart with their reflecting surfaces facing each other. An object is placed $$30\,cm$$ from the pole of either of them on their axis. If the focal lengths of both the mirrors are $$15\,cm,$$ the position of the image formed by reflection, first at the convex and then at the concave mirror, is :
A
$$19.09\,cm$$ from the pole of the concave mirror
B
$$19.09\,cm$$ from the pole of the convex mirror
C
$$11.09\,cm$$ from the pole of the concave mirror
D
$$11.09\,cm$$ from the pole of the convex mirror
Answer :
$$19.09\,cm$$ from the pole of the concave mirror
74. Interference is possible in
A
light waves only
B
sound waves only
C
Both light and sound waves
D
Neither light nor sound waves
Answer :
Both light and sound waves
75. The refractive index of the material of the prism is $$\sqrt 3 ,$$ then the angle of minimum deviation of the prism is
A
$${30^ \circ }$$
B
$${45^ \circ }$$
C
$${60^ \circ }$$
D
$${75^ \circ }$$
Answer :
$${60^ \circ }$$
76. A planoconvex lens is made of material of refractive index 1.6. The radius of curvature of the curved surface is $$60\,cm.$$ The focal length of the lens is
A
$$50\,cm$$
B
$$100\,cm$$
C
$$200\,cm$$
D
$$400\,cm$$
Answer :
$$100\,cm$$
77. There is a prism with refractive index equal to $$\sqrt 2 $$ and the refracting angle equal to $${30^ \circ }.$$ One of the refracting surface of the prism is polished. A beam of monochromatic will retrace its path if its angle of incidence over the refracting surface of the prism is
A
$${0^ \circ }$$
B
$${30^ \circ }$$
C
$${45^ \circ }$$
D
$${60^ \circ }$$
Answer :
$${45^ \circ }$$
78. Electromagnetic radiation of frequency $$v,$$ velocity $$v$$ and wavelength $$\lambda ,$$ in air, enters a glass slab of refractive index $$\mu .$$ The frequency, wavelength and velocity of light in the glass slab will be, respectively
A
$$\frac{v}{\mu },\frac{\lambda }{\mu },v$$
B
$$v,\lambda ,\frac{v}{\mu }$$
C
$$v,\frac{\lambda }{\mu },\frac{v}{\mu }$$
D
$$\frac{v}{\mu },\frac{\lambda }{\mu },\frac{v}{\mu }$$
Answer :
$$v,\frac{\lambda }{\mu },\frac{v}{\mu }$$
79.
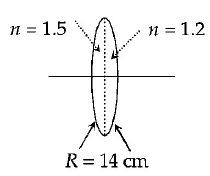
A bi - convex lens is formed with two thin plano - convex lenses as shown in the figure. Refractive index $$n$$ of the first lens is 1.5 and that of the second lens is 1.2. Both the curved surface are of the same radius of curvature $$R = 14\,cm.$$ For this biconvex lens, for an object distance of $$40\,cm,$$ the image distance will be
A
$$- 280.0\,cm$$
B
$$40.0\,cm$$
C
$$21.5\,cm$$
D
$$13.3\,cm$$
Answer :
$$40.0\,cm$$
80. A light ray travelling in glass medium is incident on glass air interface at an angle of incidence $$\theta .$$ The reflected $$(R)$$ and transmitted $$(T)$$ intensities, both as function of $$\theta ,$$ are plotted. The correct sketch is
A
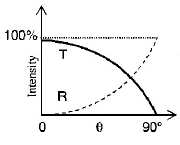

B
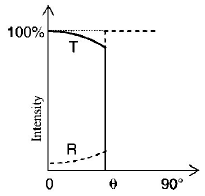

C
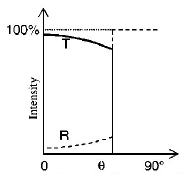

D
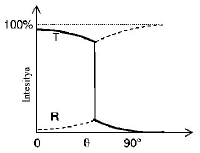

Answer :