81.
A light beam is travelling from Region I to IV (figure). The refractive index in regionals I, II, land IV are $${n_0},\frac{{{n_0}}}{2},\frac{{{n_0}}}{6}$$ and $$\frac{{{n_0}}}{8}$$ respectively. The angle of incidence $$\theta $$ for which the beam just misses entering region IV is —
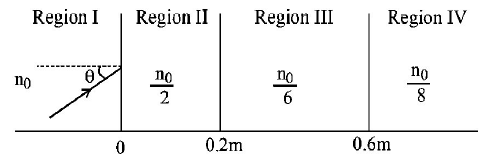
A
$${\sin ^{ - 1}}\left( {\frac{3}{4}} \right)$$
B
$${\sin ^{ - 1}}\left( {\frac{1}{8}} \right)$$
C
$${\sin ^{ - 1}}\left( {\frac{1}{4}} \right)$$
D
$${\sin ^{ - 1}}\left( {\frac{1}{3}} \right)$$
Answer :
$${\sin ^{ - 1}}\left( {\frac{1}{8}} \right)$$
82.
A point source of light $$B$$ is placed at a distance $$L$$ in front of the centre of a mirror of width $$'d'$$ hung vertically on a wall. A man walks in front of the mirror along a line parallel to the mirror at a distance $$2L$$ from it as shown in fig. The greatest distance over which he can see the image of the light source in the mirror is
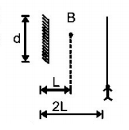
A
$$\frac{d}{2}$$
B
$$d$$
C
$$2d$$
D
$$3d$$
Answer :
$$3d$$
83.
A convex lens, of focal length $$30\,cm,$$ a concave lens of focal length $$120\,cm,$$ and a plane mirror are arranged as shown. For an object kept at a distance of $$60\,cm$$ from the convex lens, the final image, formed by the combination, is a real image, at a distance of :

A
$$60\,cm$$ from the convex lens
B
$$60\,cm$$ from the concave lens
C
$$70\,cm$$ from the convex lens
D
$$70\,cm$$ from the concave lens
Answer :
$$60\,cm$$ from the convex lens
84. An astronomical telescope of ten-fold angular magnification has a length of $$44\,cm.$$ The focal length of the objective is
A
$$440\,cm$$
B
$$44\,cm$$
C
$$40\,cm$$
D
$$4\,cm$$
Answer :
$$40\,cm$$
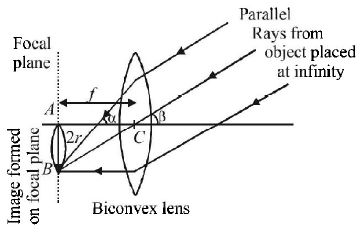
85. Rays of light from Sun falls on a biconvex lens of focal length $$f$$ and the circular image of Sun of radius $$r$$ is formed on the focal plane of the lens. Then
A
Area of image is $$\pi {r^2}$$ and area is directly proportional to $$f$$
B
Area of image is $$\pi {r^2}$$ and area is directly proportional to $${f^2}$$
C
Intensity of image increases if $$f$$ is increased
D
If lower half of the lens is covered with black paper area will become half
Answer :
Area of image is $$\pi {r^2}$$ and area is directly proportional to $${f^2}$$
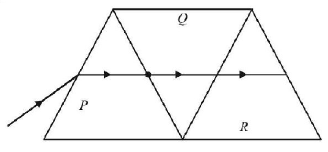
86.
A given ray of light suffers minimum deviation in an equilateral prism $$P.$$ Additional prism $$Q$$ and $$R$$ of identical shape and of the same material as $$P$$ are now added as shown in the figure. The ray will now suffer
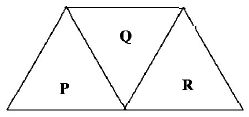
A
greater deviation
B
no deviation
C
same deviation as before
D
total internal reflection
Answer :
same deviation as before
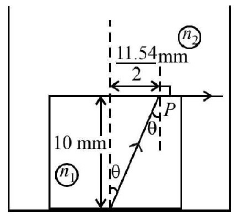
87.
A point source $$S$$ is placed at the bottom of a transparent block of height $$10\,mm$$ and refractive index 2.72. It is immersed in a lower refractive index liquid as shown in the figure. It is found that the light emerging from the block to the liquid forms a circular bright spot of diameter $$11.54\,mm$$ on the top of the block. The refractive index of the liquid is
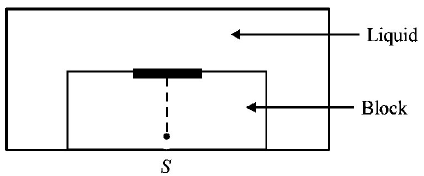
A
1.21
B
1.30
C
1.36
D
1.42
Answer :
1.36
88.
An isosceles prism of angle $${120^ \circ }$$ has a refractive index 1.44. Two parallel monochromatic rays enter the prism parallel to each other in air as shown. The rays emerge from the opposite faces

A
are parallel to each other
B
are diverging
C
make an angle $$2\left[ {{{\sin }^{ - 1}}\left( {0.72} \right) - {{30}^ \circ }} \right]$$ with each other
D
make an angle $$2{\sin ^{ - 1}}\left( {0.72} \right)$$ with each other
Answer :
make an angle $$2\left[ {{{\sin }^{ - 1}}\left( {0.72} \right) - {{30}^ \circ }} \right]$$ with each other
89. Diameter of human eye lens is $$2\,mm.$$ What will be the minimum distance between two points to resolve them, which are situated at a distance of $$50\,m$$ from eye ? [The wavelength of light is $$5000\,\mathop {\text{A}}\limits^ \circ $$ ]
A
$$2.32\,m$$
B
$$4.28\,m$$
C
$$1.25\,m$$
D
$$12.48\,m$$
Answer :
$$1.25\,m$$
90.
An object kept on the principle axis is moving in the same directions as that of mirror as shown in figure. Speed of object and mirror is $$10\,m/s$$ and $$\frac{{40}}{{12}}m/s.$$ Radius of the curvature of the mirror is $$20\,cm.$$ What should be the distance of object from the mirror at this instant so that the image is stationary?
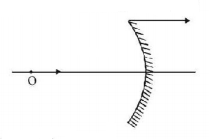
A
$$25\,cm$$
B
$$45\,cm$$
C
$$37.5\,cm$$
D
$$15\,cm$$
Answer :
$$25\,cm$$