71.
A wavefront $$AB$$ passing through a system $$C$$ emerges as $$DE.$$ The system $$C$$ could be

A
a slit
B
a biprism
C
a prism
D
a glass slab
Answer :
a prism
72. A Young’s double slit experiment uses a monochromatic source. The shape of the interference fringes formed on a screen is
A
circle
B
hyperbola
C
parabola
D
straight line
Answer :
straight line
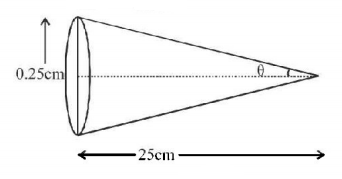
73. Assuming human pupil to have a radius of $$0.25\,cm$$ and a comfortable viewing distance of $$25\,cm,$$ the minimum separation between two objects that human eye can resolve at $$500\,nm$$ wavelength is :
A
$$100\,\mu m$$
B
$$300\,\mu m$$
C
$$1\,\mu m$$
D
$$30\,\mu m$$
Answer :
$$30\,\mu m$$
74. In a Young’s double slit experiment with light of wavelength $$\lambda ,$$ fringe pattern on the screen has fringe width $$\beta .$$ When two thin transparent glass (refractive index $$\mu $$) plates of thickness $${t_1}$$ and $${t_2}\left( {{t_1} > {t_2}} \right)$$ are placed in the path of the two beams respectively, the fringe pattern will shift by a distance
A
$$\frac{{\beta \left( {\mu - 1} \right)}}{\lambda }\left( {\frac{{{t_1}}}{{{t_2}}}} \right)$$
B
$$\frac{{\mu \beta }}{\lambda }\frac{{{t_1}}}{{{t_2}}}$$
C
$$\frac{{\beta \left( {\mu - 1} \right)}}{\lambda }\left( {{t_1} - {t_2}} \right)$$
D
$$\left( {\mu - 1} \right)\frac{\lambda }{\beta }\left( {{t_1} + {t_2}} \right)$$
Answer :
$$\frac{{\beta \left( {\mu - 1} \right)}}{\lambda }\left( {{t_1} - {t_2}} \right)$$
75.
In an interference arrangement similar to Young’s double slit experiment, the slits $${S_1}$$ and $${S_2}$$ are illuminated with coherent microwave sources, each of frequency $${10^6} Hz.$$ The sources are synchronized to have zero phase difference. The slits are separated by a distance $$d = 150.0\,m.$$ The intensity $$I\left( \theta \right)$$ is measured as a function of $$\theta ,$$ where $$\theta $$ is defined as shown. If $${I_0}$$ is the maximum intensity, then $$I\left( \theta \right)$$ for $$0 \leqslant \theta \leqslant {90^ \circ }$$ is given by

A
$$I\left( \theta \right) = \frac{{{I_0}}}{2}\,\,{\text{for }}\theta = {30^ \circ }$$
B
$$I\left( \theta \right) = \frac{{{I_0}}}{4}\,\,{\text{for }}\theta = {90^ \circ }$$
C
$$I\left( \theta \right) = {{{I_0}}}\,\,{\text{for }}\theta = {0^ \circ }$$
D
$$I\left( \theta \right)$$ is constant for all values of $$\theta .$$
Answer :
$$I\left( \theta \right) = {{{I_0}}}\,\,{\text{for }}\theta = {0^ \circ }$$
76. A wedged shaped air film having an angle of $$40$$ second is illuminated by a monochromatic light and the fringes are observed vertically down through a microscope. The fringe separation between two consecutive bright fringes is $$0.12\,cm.$$ The wavelength of light is :
A
$$5545\,\mathop {\text{A}}\limits^ \circ $$
B
$$6025\,\mathop {\text{A}}\limits^ \circ $$
C
$$4925\,\mathop {\text{A}}\limits^ \circ $$
D
$$4655\,\mathop {\text{A}}\limits^ \circ $$
Answer :
$$4655\,\mathop {\text{A}}\limits^ \circ $$
77. An observer is moving with half the speed of light towards a stationary microwave source emitting waves at frequency $$10\,GHz.$$ What is the frequency of the microwave measured by the observer? (speed of light $$ = 3 \times {10^8}m{s^{ - 1}}$$ )
A
$$17.3\,GHz$$
B
$$15.3\,GHz$$
C
$$10.1\,GHz$$
D
$$12.1\,GHz$$
Answer :
$$17.3\,GHz$$
78. In the ideal double-slit experiment, when a glass-plate (refractive index $$1.5$$) of thickness $$t$$ is introduced in the path of one of the interfering beams (wave-length $$\lambda $$), the intensity at the position where the central maximum occurred previously remains unchanged. The minimum thickness of the glass-plate is
A
$$2\lambda $$
B
$$\frac{{2\lambda }}{3}$$
C
$$\frac{{\lambda }}{3}$$
D
$$\lambda $$
Answer :
$$2\lambda $$
79. An electromagnetic wave in vacuum has the electric and magnetic field $$\overrightarrow E $$ and $$\overrightarrow B ,$$ which are always perpendicular to each other. The direction of polarization is given by $$\overrightarrow X $$ and that of wave propagation by $$\overrightarrow k .$$ Then
A
$$\overrightarrow X \parallel \overrightarrow B \,\,{\text{and }}\overrightarrow k \parallel \overrightarrow B \times \overrightarrow E $$
B
$$\overrightarrow X \parallel \overrightarrow E \,\,{\text{and }}\overrightarrow k \parallel \overrightarrow E \times \overrightarrow B $$
C
$$\overrightarrow X \parallel \overrightarrow B \,\,{\text{and }}\overrightarrow k \parallel \overrightarrow E \times \overrightarrow B $$
D
$$\overrightarrow X \parallel \overrightarrow E \,\,{\text{and }}\overrightarrow k \parallel \overrightarrow B \times \overrightarrow E $$
Answer :
$$\overrightarrow X \parallel \overrightarrow E \,\,{\text{and }}\overrightarrow k \parallel \overrightarrow E \times \overrightarrow B $$
80. Two coherent monochromatic light beams of intensities $$I$$ and $$4\,I$$ are superposed. The maximum and minimum possible intensities in the resulting beam are
A
$$5\,I$$ and $$I$$
B
$$5\,I$$ and $$3\,I$$
C
$$9\,I$$ and $$I$$
D
$$9\,I$$ and $$3\,I$$
Answer :
$$9\,I$$ and $$I$$