81. To produce a minimum reflection of wavelengths near the middle of visible spectrum $$\left( {550\,nm} \right),$$ how thick should a coating of $$Mg{F_2}\left( {\mu = 1.38} \right)$$ coated on a glass surface?
A
$${10^{ - 7}}m$$
B
$${10^{ - 10}}m$$
C
$${10^{ - 9}}m$$
D
$${10^{ - 8}}m$$
Answer :
$${10^{ - 7}}m$$
82. The maximum number of possible interference maxima for slit-separation equal to twice the wavelength in Young’s double - slit experiment is
A
three
B
five
C
infinite
D
zero
Answer :
five
83.
A $$YDSE$$ is conducted in water $$\left( {{\mu _1}} \right)$$ as shown in figure. A glass plate of thickness $$t$$ and refractive index $${{\mu _2}}$$ is placed in the path of $${S_2}.$$ The optical path difference at $$O$$ is
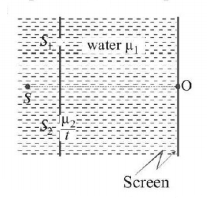
A
$$\left( {{\mu _2} - 1} \right)t$$
B
$$\left( {{\mu _1} - 1} \right)t$$
C
$$\left( {\frac{{{\mu _2}}}{{{\mu _1}}} - 1} \right)t$$
D
$$\left( {{\mu _2} - {\mu _1}} \right)t$$
Answer :
$$\left( {{\mu _2} - {\mu _1}} \right)t$$
84. A possible means for making an airplane invisible to radar is to coat the plane with an anti reflective polymer. Radar waves have a wavelength of $$3.00\,cm$$ and the index of refraction of the polymer is $$n = 1.50.$$ How thick would you make the coating?
A
$$1.50\,cm$$
B
$$3.00\,cm$$
C
$$0.50\,cm$$
D
None of these
Answer :
$$0.50\,cm$$
85. A plastic sheet (refractive index $$= 1.6$$ ) covers one slit of a double slit arrangement meant for the Young's experiment. When the double slit is illuminated by monochromatic light (wavelength in air $$6600\,\mathop {\text{A}}\limits^ \circ $$ ), the centre of the screen appears dark rather than bright. The minimum thickness of the plastic sheet to be used for this to happen is:
A
$$3300\,\mathop {\text{A}}\limits^ \circ $$
B
$$6600\,\mathop {\text{A}}\limits^ \circ $$
C
$$2062\,\mathop {\text{A}}\limits^ \circ $$
D
$$5500\,\mathop {\text{A}}\limits^ \circ $$
Answer :
$$5500\,\mathop {\text{A}}\limits^ \circ $$
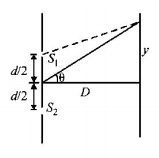
86.
In an interference arrangement similar to Young’s double-slit experiment, the slits $${S_1}$$ and $${S_2}$$ are illuminated with coherent microwave sources, each of frequency $${10^6}Hz.$$ The sources are synchronized to have zero phase difference. The slits are separated by a distance $$d = 150.0\,m.$$ The intensity $$I\left( \theta \right)$$ is measured as a function of $$\theta ,$$ where $$\theta $$ is defined as shown. If $${I_0}$$ is the maximum intensity, then $$I\left( \theta \right)$$ for $$0 \leqslant \theta \leqslant {90^ \circ }$$ is given by

A
$$I\left( \theta \right) = \frac{{{I_0}}}{2}\,{\text{for}}\,\theta = {30^ \circ }$$
B
$$I\left( \theta \right) = \frac{{{I_0}}}{4}\,{\text{for}}\,\theta = {90^ \circ }$$
C
$$I\left( \theta \right) = {I_0}\,{\text{for}}\,\theta = {0^ \circ }$$
D
$$I\left( \theta \right)$$ is constant for all values of $$\theta .$$
Answer :
$$I\left( \theta \right) = {I_0}\,{\text{for}}\,\theta = {0^ \circ }$$
87.
An initially parallel cylindrical beam travels in a medium of refractive index $$\mu \left( I \right) = {\mu _0} + {\mu _2}I,$$ where $${\mu _0}$$ and $${\mu _2}$$ are positive constants and $$I$$ is the intensity of the light beam. The intensity of the beam is decreasing with increasing radius.
The initial shape of the wave front of the beam is
A
convex
B
concave
C
convex near the axis and concave near the periphery
D
planar
Answer :
planar
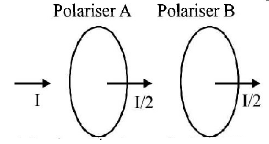
88. Unpolarized light of intensity $$I$$ passes through an ideal polarizer $$A.$$ Another indentical polarizer $$B$$ is placed behind $$A.$$ The intensity of light beyond $$B$$ is found to be $$\frac{I}{2}.$$ Now another identical polarizer $$C$$ is placed between $$A$$ and $$B.$$ The intensity beyond $$B$$ is now found to be $$\frac{I}{8}.$$ The angle between polarizer $$A$$ and $$C$$ is:
A
$${0^ \circ }$$
B
$${30^ \circ }$$
C
$${45^ \circ }$$
D
$${60^ \circ }$$
Answer :
$${45^ \circ }$$
89. In a Young’s double slit experiment, 12 fringes are observed to be formed in a certain segment of the screen when light of wavelength $$600\,nm$$ is used. If the wavelength of light is changed to $$400\,nm,$$ number of fringes observed in the same segment of the screen is given by
A
12
B
18
C
24
D
30
Answer :
18
90. Interference fringes were produced in Young's double slit experiment using light of wavelength $$5000\,\mathop {\text{A}}\limits^ \circ .$$ When a film of material $$2.5 \times {10^{ - 3}}cm$$ thick was placed over one of the slits, the fringe pattern shifted by a distance equal to $$20$$ fringe width. The refractive index of the material of the film is
A
1.25
B
1.33
C
1.4
D
1.5
Answer :
1.4