1. A block connected to a spring oscillates vertically. A damping force $${F_d},$$ acts on the block by the surrounding medium. Given as $${F_d} = - bVb$$ is a positive constant which depends on :
A
viscosity of the medium
B
size of the block
C
shape of the block
D
All of these
Answer :
All of these
2. A particle, with restoring force proportional to displacement and resisting force proportional to velocity is subjected to a force $$F\sin \omega t.$$ If the amplitude of the particle is maximum for $$\omega = {\omega _1}$$ and the energy of the particle is maximum for $$\omega = {\omega _2},$$ then
A
$${\omega _1} = {\omega _0}\,\,{\text{and}}\,\,{\omega _2} \ne {\omega _0}$$
B
$${\omega _1} = {\omega _0}\,\,{\text{and}}\,\,{\omega _2} = {\omega _0}$$
C
$${\omega _1} \ne {\omega _0}\,\,{\text{and}}\,\,{\omega _2} = {\omega _0}$$
D
$${\omega _1} \ne {\omega _0}\,\,{\text{and}}\,\,{\omega _2} \ne {\omega _0}$$
Answer :
$${\omega _1} \ne {\omega _0}\,\,{\text{and}}\,\,{\omega _2} = {\omega _0}$$
3. A simple pendulum oscillates in air with time period $$T$$ and amplitude $$A.$$ As the time passes
A
$$T$$ and $$A$$ both decrease
B
$$T$$ increases and $$A$$ is constant
C
$$T$$ remains same and $$A$$ decreases
D
$$T$$ decreases and $$A$$ is constant
Answer :
$$T$$ remains same and $$A$$ decreases
4. If a particle takes $$0.5\,\sec$$ to reach position of minimum velocity from previous such position, then
A
$$T = 6\,\sec ,\,v = \frac{1}{6}\,Hz$$
B
$$T = 2\,\sec ,\,v = 1\,Hz$$
C
$$T = 3\,\sec ,\,v = 3\,Hz$$
D
$$T = 1\,\sec ,\,v = 1\,Hz$$
Answer :
$$T = 1\,\sec ,\,v = 1\,Hz$$
5.
A bent tube of uniform cross-section area $$A$$ has a non-viscous liquid of density $$\rho .$$ The mass of liquid in the tube is $$m.$$ The time period of oscillation of the liquid is
A
$$2\pi \sqrt {\frac{m}{{\rho gA}}} $$
B
$$2\pi \sqrt {\frac{m}{{2\rho gA}}} $$
C
$$2\pi \sqrt {\frac{{2m}}{{\rho gA}}} $$
D
None of these
Answer :
$$2\pi \sqrt {\frac{m}{{\rho gA}}} $$
6. A linear harmonic oscillator of force constant $$2 \times {10^6}N/m$$ and amplitude $$0.01\,m$$ has a total mechanical energy of $$160\,J.$$ Its
A
maximum potential energy is $$160\,J$$
B
maximum potential energy is $$100\,J$$
C
maximum potential energy is zero
D
minimum potential energy is $$100\,J$$
Answer :
maximum potential energy is $$160\,J$$
7. The amplitude of a damped oscillator decreases to 0.9 times its original magnitude in $$5s.$$ In another $$10s$$ it will decrease to $$\alpha $$ times its original magnitude, where $$\alpha $$ equals
A
0.7
B
0.81
C
0.729
D
0.6
Answer :
0.729
8. A simple pendulum performs simple harmonic motion about $$x = 0$$ with an amplitude $$a$$ and time period $$T.$$ The speed of the pendulum at $$x = \frac{a}{2}$$ will be
A
$$\frac{{\pi a\sqrt 3 }}{{2T}}$$
B
$$\frac{{\pi a}}{T}$$
C
$$\frac{{3{\pi ^2}a}}{T}$$
D
$$\frac{{\pi a\sqrt 3 }}{T}$$
Answer :
$$\frac{{\pi a\sqrt 3 }}{T}$$
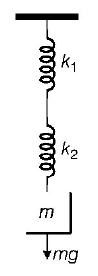
9. A mass $$m$$ is suspended from the two coupled springs connected in series. The force constant for springs are $${k_1}$$ and $${k_2}.$$ The time period of the suspended mass will be
A
$$T = 2\pi \sqrt {\frac{m}{{{k_1} - {k_2}}}} $$
B
$$T = 2\pi \sqrt {\frac{{m{k_1}{k_2}}}{{{k_1} + {k_2}}}} $$
C
$$T = 2\pi \sqrt {\frac{m}{{{k_1} + {k_2}}}} $$
D
$$T = 2\pi \sqrt {\frac{{m\left( {{k_1} + {k_2}} \right)}}{{{k_1}{k_2}}}} $$
Answer :
$$T = 2\pi \sqrt {\frac{{m\left( {{k_1} + {k_2}} \right)}}{{{k_1}{k_2}}}} $$
10. Which of the following is true about total mechanical energy of $$SHM$$ ?
A
It is zero at mean position.
B
It is zero at extreme position.
C
It is always zero.
D
It is never zero.
Answer :
It is never zero.