151.
The $$x - t$$ graph of a particle undergoing simple harmonic motion is shown below. The acceleration of the particle at $$t = \frac{4}{3}s$$ is
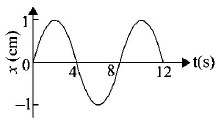
A
$$\frac{{\sqrt 3 }}{{32}}{p^2}cm/{s^2}$$
B
$$\frac{{ - {\pi ^2}}}{{32}}cm/{s^2}$$
C
$$\frac{{{\pi ^2}}}{{32}}cm/{s^2}$$
D
$$ - \frac{{\sqrt 3 }}{{32}}{\pi ^2}cm/{s^2}$$
Answer :
$$ - \frac{{\sqrt 3 }}{{32}}{\pi ^2}cm/{s^2}$$
152.
Out of the following functions representing motion of a particle which represents $$SHM$$ ?
$$\eqalign{
& {\text{I}}{\text{.}}\,y = \sin \,\omega t - \cos \,\omega t \cr
& {\text{II}}{\text{.}}\,y = {\sin ^3}\,\omega t \cr
& {\text{III}}{\text{.}}\,y = 5\cos \left( {\frac{{3\pi }}{4} - 3\omega t} \right) \cr
& {\text{IV}}{\text{.}}\,y = 1 + \omega t + {\omega ^2}{t^2} \cr} $$
A
Only (IV) does not represent $$SHM$$
B
(I) and (III)
C
(I) and (II)
D
Only (I)
Answer :
(I) and (III)
153. Two particles execute $$SHM$$ on same straight line with same mean position, same time period 6 second and same amplitude $$5\,cm.$$ Both the particles start $$SHM$$ from their mean position (in same direction) with a time gap of 1 second. The maximum separation between the two particles during their motion is
A
$$2\,cm$$
B
$$3\,cm$$
C
$$4\,cm$$
D
$$5\,cm$$
Answer :
$$5\,cm$$
154.
The amplitude of velocity of a particle is given by, $${V_m} = \frac{{{V_0}}}{{\left( {a{\omega ^2} - b\omega + c} \right)}}$$ where $${V_0},a,b$$ and $$c$$ are positive :
The condition for a single resonant frequency is
A
$${b^2} < 4ac$$
B
$${b^2} = 4ac$$
C
$${b^2} = 5ac$$
D
$${b^2} = 7ac$$
Answer :
$${b^2} = 4ac$$
155. A forced oscillator is acted upon by a force $$F = {F_0}\sin \omega t.$$ The amplitude of oscillation is given by $$\frac{{55}}{{\sqrt {2{\omega ^2} - 36\omega + 9} }}.$$ The resonant angular frequency is
A
2 unit
B
9 unit
C
18 unit
D
36 unit
Answer :
9 unit
156. The displacement of a particle varies according to the relation $$x = 4\left( {\cos \pi t + \sin \pi t} \right).$$ The amplitude of the particle is
A
-4
B
4
C
$$4\sqrt 2 $$
D
8
Answer :
$$4\sqrt 2 $$
157. An air column, closed at one end and open at the other, resonates with a tunning fork when the smallest length of the column is $$50\,cm.$$ The next larger length of the column resonating with the same tunning fork is
A
$$100\,cm$$
B
$$150\,cm$$
C
$$200\,cm$$
D
$$66.7\,cm$$
Answer :
$$150\,cm$$
158.
For a simple pendulum, a graph is plotted between its kinetic
energy $$\left( {KE} \right)$$ and potential energy $$\left( {PE} \right)$$ against its displacement $$d.$$ Which one of the following represents these correctly?
(graphs are schematic and not drawn to scale)
A
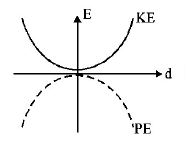

B
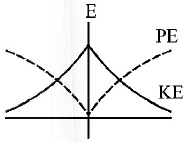

C
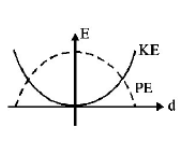

D
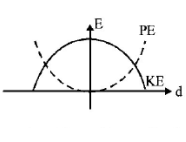

Answer :


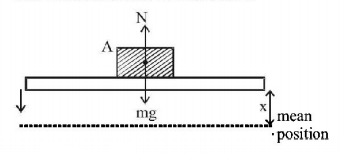
159. A coin is placed on a horizontal platform which undergoes vertical simple harmonic motion of angular frequency $$\omega .$$ The amplitude of oscillation is gradually increased. The coin will leave contact with the platform for the first time
A
at the mean position of the platform
B
for an amplitude of $$\frac{g}{{{\omega ^2}}}$$
C
for an amplitude of $$\frac{{{g^2}}}{{{\omega ^2}}}$$
D
at the highest position of the platform
Answer :
for an amplitude of $$\frac{g}{{{\omega ^2}}}$$
160. The phase difference between the instantaneous velocity and acceleration of a particle executing simple harmonic motion is
A
$$\pi $$
B
$$0.707\,\pi $$
C
zero
D
$$0.5\,\pi $$
Answer :
$$0.5\,\pi $$