Waves MCQ Questions & Answers in Oscillation and Mechanical Waves | Physics

From law of length, the frequency of vibrating string is inversely proportional to its length,
\[{\text{i}}{\text{.e}}{\text{.}}\,\,n \propto \frac{1}{l}\,\,\left[ {\begin{array}{*{20}{c}} {n = {\text{frequency of string}}} \\ {l = {\text{length of string}}} \end{array}} \right]\]
$$\eqalign{ & {\text{or}}\,\,nl = {\text{constant}}\left( {{\text{say}}\,k} \right) \cr & {\text{or}}\,\,l = \frac{k}{n} \cr} $$
The segments of string of length $${l_1},{l_2},{l_3},\,....$$   have frequencies $${n_1},{n_2},{n_3},\,....$$
Total length of string is $$l.$$
$$\eqalign{ & {\text{So,}}\,\,l = {l_1} + {l_2} + {l_3} + \,.... \cr & \therefore \frac{k}{n} = \frac{k}{{{n_1}}} + \frac{k}{{{n_2}}} + \frac{k}{{{n_3}}} + \,.... \cr & {\text{or}}\,\,\frac{1}{n} = \frac{1}{{{n_1}}} + \frac{1}{{{n_2}}} + \frac{1}{{{n_3}}} + \,.... \cr} $$

$$\eqalign{ & {v_P} < v \cr & {\text{or}}\,\,\omega A < f\lambda \,\,{\text{or}}\,\,A < \frac{{f\lambda }}{\omega }\,\,{\text{or}}\,\,\frac{\lambda }{{2\pi }} \cr} $$

If $$x$$ be the distance of epicentre from the seismograph, then
$$\eqalign{ & \frac{x}{{{v_s}}} - \frac{x}{{{v_p}}} = 4 \times 60\,\,{\text{or}}\,\,\frac{x}{{4.5}} - \frac{x}{8} = 4 \times 60\,\,{\text{on}}\,{\text{simplifying, we get}} \cr & x = 2500\,km \cr} $$

After $$2\,s,$$  the each wave travels a distance $$ = 2 \times 2 = 4\,m.$$
The wave shape is shown in figure.
Thus energy is purely kinetic.

$$\eqalign{ & n' = n\left[ {\frac{{v + {v_0}}}{v}} \right] \cr & = n\left[ {\frac{{v + \frac{v}{5}}}{v}} \right] \cr & = n\left[ {\frac{6}{5}} \right] \cr & \frac{{n'}}{n} = \frac{6}{5}; \cr & \frac{{n' - n}}{n} = \frac{{6 - 5}}{5} \times 100 \cr & = 20\% \cr} $$

In a closed organ pipe, only alternate harmonics of frequencies $${v_1},3{v_1},5{v_1},....$$   etc are present. The harmonics of frequencies $$2{v_1},4{v_1},6{v_1},....$$   are missing. In general, the frequency of note produced in n^th normal mode of vibration of closed organ pipe would be
$${v_n} = \frac{{\left( {2n - 1} \right)v}}{{4L}} = \left( {2n - 1} \right){v_1}$$
This is $${\left( {2n - 1} \right)}$$  th harmonic or $$\left( {n - 1} \right)$$  th overtone. Third overtone has a frequency $$7\,{\nu _1},$$  which means
$$L = \frac{{7\lambda }}{4} = \frac{\lambda }{2} + \frac{\lambda }{2} + \frac{\lambda }{2} + \frac{\lambda }{4}$$
Which is three full loops and a half loop, which is equal to four nodes and four antinodes.

$$\eqalign{ & {n_1} = \frac{1}{{2\,\ell }}\sqrt {\left( {\frac{T}{{4\,\pi {r^2}\rho }}} \right)} \,\,{\text{and }}{n_2} = \frac{1}{{4\,\ell }}\sqrt {\left( {\frac{T}{{\pi {r^2}\rho }}} \right)} \cr & n = \frac{v}{\lambda } = \frac{1}{\lambda }\sqrt {\frac{T}{m}} \,\,\left[ {{\text{where }}\frac{\lambda }{2} = {\text{length of string}}} \right] \cr & \therefore \,\,\frac{{{n_1}}}{{{n_2}}} = 2 \times \frac{1}{2} = 1\left[ {\because \,\,m = \frac{{{\text{mass}}}}{{{\text{length}}}} = \frac{{\rho \times A \times {\text{length}}}}{{{\text{length}}}} = \rho A} \right] \cr} $$

$$\eqalign{ & {\text{From equation,}}\,\,\omega = 100 \cr & \therefore \frac{{2\pi }}{T} = 100 \Rightarrow \nu = \frac{{100}}{{2\pi }} \cr & \frac{{2\pi }}{\lambda } = 20 \Rightarrow \lambda = \frac{{2\pi }}{{20}} \cr & \nu = \lambda \nu = \frac{{2\pi }}{{20}} \times \frac{{100}}{{2\pi }} = 5\,m/s \cr} $$

$$\eqalign{ & {\text{From formula,}}\,\,f = \frac{1}{x}\sqrt {\frac{T}{m}} \Rightarrow \frac{1}{f} \propto l \cr & \therefore {l_1}:{l_2}:{l_3} = \frac{1}{{{f_1}}}:\frac{1}{{{f_2}}}:\frac{1}{{{f_3}}} = {f_2}{f_3}:{f_1}{f_3}:{f_1}{f_2}\,\,\left[ {{\text{Given:}}\,{f_1}:{f_2}:{f_3} = 1:3:5} \right] \cr & = 15:5:3 \cr} $$
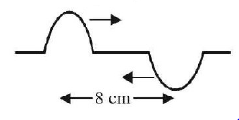
Therefore the positions of two bridges below the wire are
$$\eqalign{ & \frac{{15 \times 100}}{{15 + 5 + 3}}\,cm\,\,{\text{and}}\,\,\frac{{15 \times 100 + 5 \times 100}}{{15 + 5 + 3}}\,cm \cr & {\text{i}}{\text{.e}}{\text{.,}}\,\frac{{1500}}{{23}}\,cm,\frac{{2000}}{{23}}\,cm \cr} $$

$$\eqalign{ & {\text{Frequency}}\,\,v = \frac{1}{{2L}}\sqrt {\frac{T}{m}} \,\,\,\because V \propto \frac{1}{l} \cr & \therefore {l_1}:{l_2}:{l_3} = \frac{1}{1}:\frac{1}{2}:\frac{1}{3} = 6:3:2 \cr} $$