31.
Which of the following is correct increasing order of $$pH$$ of the hydroxide solution of $$T, P$$ and $$X ?$$

A
$$T < P < X$$
B
$$X < P < T$$
C
$$P < T < X$$
D
$$P < X < T$$
Answer :
$$X < P < T$$
32.
Consider some facts about group 16 elements :
(i) They are $$d$$ - block elements.
(ii) They are called chalcogens.
(iii) They have $$n{s^2}n{p^4}$$ configuration of valence shell.
Select the correct facts.
A
Both (i) and (ii)
B
Both (ii) and (iii)
C
Both (i) and (iii)
D
(i), (ii) and (iii)
Answer :
Both (ii) and (iii)
33. In which of the following arrangements, the order is NOT according to the property indicated against it?
A
$$Li < Na < K < Rb:$$ Increasing metallic radius
B
$$I < Br < F < Cl:$$ Increasing electron gain enthalpy (with negative sign)
C
$$B < C < N < O$$ Increasing first ionization enthalpy
D
$$A{l^{3 + }} < M{g^{2 + }} < N{a^ + } < {F^ - }$$ Increasing ionic size
Answer :
$$B < C < N < O$$ Increasing first ionization enthalpy
34. Which one of the following statements is incorrect ?
A
Greater the nuclear charge, greater is the electron affinity
B
Nitrogen has zero electron affinity
C
Electron affinity decreases from fluorine to iodine in 17th group
D
Chlorine has highest electron affinity
Answer :
Electron affinity decreases from fluorine to iodine in 17th group
35. An atom has electronic configuration $$1{s^2},2{s^2}2{p^6},3{s^2}3{p^6}3{d^3},4{s^2},$$ you will place it in
A
fifth group
B
fifteenth group
C
second group
D
third group
Answer :
fifth group
36.
The electron affinity of chlorine is $$3.7\,eV.\,1\,g$$ of chlorine is completely converted to $$C{l^ - }\,ion$$ in a gaseous state. $$\left( {1\,eV = 23.06\,kcal\,mo{l^{ - 1}}} \right).$$
Energy released in the process is
A
$$4.8\,kcal$$
B
$$7.2\,kcal$$
C
$$8.2\,kcal$$
D
$$2.4\,kcal$$
Answer :
$$2.4\,kcal$$
37. An element has the electronic configuration $$1{s^2}2{s^2}2{p^6}3{s^2}3{p^6}3{d^8}4{s^2}.$$ What will be its position in the periodic table?
A
Period 4, Group 10
B
Period 2, Group 2
C
Period 4, Group 2
D
Period 2, Group 8
Answer :
Period 4, Group 10
38. In the periodic table, with the increase in atomic number, the metallic character of an element
A
decrease in a period and increases in a group
B
increases in a period and decreases in a group
C
increases in a period as well as in the group
D
decreases in a period and also in the group
Answer :
decrease in a period and increases in a group
39. Which of the following oxides is neutral in nature?
A
$$SrO$$
B
$$A{l_2}{O_3}$$
C
$$C{O_2}$$
D
$$CO$$
Answer :
$$CO$$
40.
Few elements are matched with their successive ionisation energies. Identify the elements.
| Element | $$I{E_1}\left( {kJ/mol} \right)$$ | $$I{E_2}\left( {kJ/mol} \right)$$ |
|---|---|---|
| $$X$$ | 2372 | 5251 |
| $$Y$$ | 520 | 7297 |
| $$Z$$ | 900 | 1758 |
| $$X$$ | $$Y$$ | $$Z$$ | |
| (a) | Noble gas | Alkali metal | Alkaline earth metal |
| (b) | Alkali metal | A noble gas | Alkaline earth metal |
| (c) | Alkaline earth metal | Alkali metal | A noble gas |
| (d) | Alkali metal | Alkaline earth metal | A noble gas |
A
(a)
B
(b)
C
(c)
D
(d)
Answer :
(a)
 Stable configuration
Stable configuration 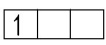 Unstable configuration
Unstable configuration 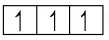 Stable configuration (half-filled)
Stable configuration (half-filled) 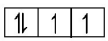 Unstable configuration
Unstable configuration