81. Suppose $$f\left( x \right) = {e^{ax}} + {e^{bx}},$$ where $$a \ne b,$$ and that $$f''\left( x \right) - 2f'\left( x \right) - 15f\left( x \right) = 0$$ for all $$x.$$ Then the product $$ab$$ is :
A
$$25$$
B
$$9$$
C
$$ - 15$$
D
$$ - 9$$
Answer :
$$ - 15$$
82.
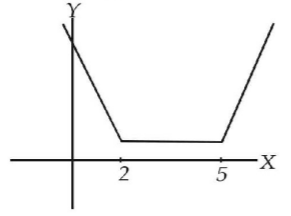
Consider the function, $$f\left( x \right) = \left| {x - 2} \right| + \left| {x - 5} \right|,\,x \in \,R.$$
Statement-1 : $$f'\left( 4 \right) = 0$$
Statement-2 : $$f$$ is continuous in [2, 5], differentiable in (2, 5) and $$f\left( 2 \right) = f\left( 5 \right).$$
A
Statement-1 is false, Statement-2 is true.
B
Statement-1 is true, statement-2 is true; statement-2 is a correct explanation for Statement-1.
C
Statement-1 is true, statement-2 is true; statement-2 is not a correct explanation for Statement-1.
D
Statement-1 is true, statement-2 is false.
Answer :
Statement-1 is true, statement-2 is true; statement-2 is not a correct explanation for Statement-1.
83. If $$y = {\cot ^{ - 1}}\left[ {\frac{{\sqrt {1 + \sin \,x} + \sqrt {1 - \sin \,x} }}{{\sqrt {1 + \sin \,x} - \sqrt {1 - \sin \,x} }}} \right]$$ where $$0 < x < \frac{x}{2},$$ then $$\frac{{dy}}{{dx}}$$ is equal to :
A
$$\frac{1}{2}$$
B
$$2$$
C
$$\sin \,x + \cos \,x$$
D
$$\sin \,x - \cos \,x$$
Answer :
$$\frac{1}{2}$$
84. If $$y = \sin \,2x$$ then $$\frac{{{d^6}y}}{{d{x^6}}}$$ at $$x = \frac{\pi }{2}$$ is equal to :
A
$$-64$$
B
$$0$$
C
$$64$$
D
none of these
Answer :
$$0$$
85. If $$y = {\left( {1 + \frac{1}{x}} \right)^x}$$ then $$\frac{{2\sqrt {{y_2}\left( 2 \right) + \frac{1}{8}} }}{{\left( {\log \frac{3}{2} - \frac{1}{3}} \right)}}$$ is equal to -
A
3
B
4
C
1
D
2
Answer :
3
86. If $$f''\left( x \right) = - f\left( x \right)$$ and $$g\left( x \right) = f'\left( x \right)$$ and $$F\left( x \right) = {\left( {f\left( {\frac{x}{2}} \right)} \right)^2} + {\left( {g\left( {\frac{x}{2}} \right)} \right)^2}$$ and given that $$F\left( 5 \right) = 5,$$ then $$F\left( {10} \right)$$ is equal to :
A
5
B
10
C
0
D
15
Answer :
5
87. If $$f\left( x \right) = \left| {1 - x} \right|,$$ then the points where $${\sin ^{ - 1}}\left( {f\left| x \right|} \right)$$ is non-differentiable are :
A
$$\left\{ {0,\,1} \right\}$$
B
$$\left\{ {0,\, - 1} \right\}$$
C
$$\left\{ {0,\,1,\, - 1} \right\}$$
D
none of these
Answer :
$$\left\{ {0,\,1,\, - 1} \right\}$$
88. If $$y = {\cos ^{ - 1}}\left( {\cos \,x} \right)$$ then $$\frac{{dy}}{{dx}}$$ at $$x = \frac{{5\pi }}{4}$$ is equal to :
A
1
B
$$-1$$
C
$$\frac{1}{{\sqrt 2 }}$$
D
none of these
Answer :
$$-1$$
89. If $${y^2} = P\left( x \right) = a$$ polynomial of degree 3 then $$2\frac{d}{{dx}}\left( {{y^3}\frac{{{d^2}y}}{{d{x^2}}}} \right)$$ equals :
A
$$P'''\left( x \right) + P'\left( x \right)$$
B
$$P''\left( x \right).P'''\left( x \right)$$
C
$$P\left( x \right).P'''\left( x \right)$$
D
none of these
Answer :
$$P\left( x \right).P'''\left( x \right)$$
90.
If for all $$x,\,y$$ the function $$f$$ is defined by
$$f\left( x \right) + f\left( y \right) + f\left( x \right).f\left( y \right) = 1$$ and $$f\left( x \right) > 0$$ then :
A
$$f'\left( x \right)$$ does not exist
B
$$f'\left( x \right) = 0$$ for all $$x$$
C
$$f'\left( 0 \right) < f'\left( 1 \right)$$
D
none of these
Answer :
$$f'\left( x \right) = 0$$ for all $$x$$