31. The number of values of $$m$$ for which the line $$y = mx + \sqrt {{m^2} - 4} $$ touches the hyperbola $$4\left( {{x^2} - 1} \right) = {y^2}$$ is :
A
two
B
zero
C
one
D
infinite
Answer :
infinite
32. For the Hyperbola $$\frac{{{x^2}}}{{{{\cos }^2}\alpha }} - \frac{{{y^2}}}{{{{\sin }^2}\alpha }} = 1,$$ which of the following remains constant when $$\alpha $$ varies $$=?$$
A
abscissae of vertices
B
abscissae of foci
C
eccentricity
D
directrix
Answer :
abscissae of foci
33. Equation of the latus rectum of the hyperbola $${\left( {10x - 5} \right)^2} + {\left( {10y - 2} \right)^2} = 9{\left( {3x + 4y - 7} \right)^2}{\text{ is :}}$$
A
$$y - \frac{1}{5} = - \frac{3}{4}\left( {x - \frac{1}{2}} \right)$$
B
$$x - \frac{1}{5} = - \frac{3}{4}\left( {y - \frac{1}{2}} \right)$$
C
$$y + \frac{1}{5} = - \frac{3}{4}\left( {x + \frac{1}{2}} \right)$$
D
$$x + \frac{1}{5} = - \frac{3}{4}\left( {y + \frac{1}{2}} \right)$$
Answer :
$$y - \frac{1}{5} = - \frac{3}{4}\left( {x - \frac{1}{2}} \right)$$
34. The number of points $$\left( {a,\,b} \right),$$ where $$a$$ and $$b$$ are positive integers lying on the hyperbola $${x^2} - {y^2} = 512$$ is :
A
$$3$$
B
$$4$$
C
$$5$$
D
$$6$$
Answer :
$$4$$
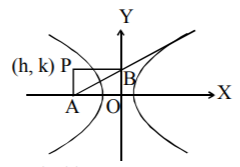
35. Tangents at any point on the hyperbola $$\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1$$ cut the axes at $$A$$ and $$B$$ respectively. If the rectangle $$OAPB$$ (where $$O$$ is the origin) is completed, then locus of point $$P$$ is given by :
A
$$\frac{{{a^2}}}{{{x^2}}} - \frac{{{b^2}}}{{{y^2}}} = 1$$
B
$$\frac{{{a^2}}}{{{x^2}}} + \frac{{{b^2}}}{{{y^2}}} = 1$$
C
$$\frac{{{a^2}}}{{{y^2}}} - \frac{{{b^2}}}{{{x^2}}} = 1$$
D
None of these
Answer :
$$\frac{{{a^2}}}{{{x^2}}} - \frac{{{b^2}}}{{{y^2}}} = 1$$
36. A hyperbola having the transverse axis of length $$2\,\sin \,\theta ,$$ is confocal with the ellipse $$3{x^2} + 4{y^2} = 12.$$ Then its equation is :
A
$${x^2}{\text{cose}}{{\text{c}}^2}\theta - {y^2}{\sec ^2}\theta = 1$$
B
$${x^2}{\sec ^2}\theta - {y^2}{\text{cose}}{{\text{c}}^2}\theta = 1$$
C
$${x^2}{\sin ^2}\theta - {y^2}{\cos ^2}\theta = 1$$
D
$${x^2}{\cos ^2}\theta - {y^2}{\sin ^2}\theta = 1$$
Answer :
$${x^2}{\text{cose}}{{\text{c}}^2}\theta - {y^2}{\sec ^2}\theta = 1$$
37. The locus of a point $$P\left( {\alpha ,\,\beta } \right)$$ moving under the condition that the line $$y = \alpha x + \beta $$ is a tangent to the hyperbola $$\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1$$ is :
A
a circle
B
an ellipse
C
a hyperbola
D
a parabola
Answer :
a hyperbola