61.
The $$r.m.s.$$ value of potential difference $$V$$ shown in the figure is
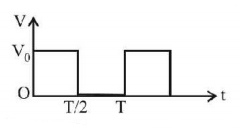
A
$${V_0}$$
B
$$\frac{{{V_0}}}{{\sqrt 2 }}$$
C
$$\frac{{{V_0}}}{2}$$
D
$$\frac{{{V_0}}}{{\sqrt 3 }}$$
Answer :
$$\frac{{{V_0}}}{{\sqrt 2 }}$$
62. In an $$AC$$ circuit with voltage $$V$$ and current $$i$$ the power dissipated is
A
Depends on the phase between $$V$$ and $$i$$
B
$$\frac{1}{{\sqrt 2 }}Vi$$
C
$$\frac{1}{2}Vi$$
D
$$Vi$$
Answer :
Depends on the phase between $$V$$ and $$i$$
63. In a $$LCR$$ circuit capacitance is changed from $$C$$ to $$2 C.$$ For the resonant frequency to remain unchanged, the inductance should be changed from $$L$$ to
A
$$\frac{L}{2}$$
B
$$2L$$
C
$$4L$$
D
$$\frac{L}{4}$$
Answer :
$$\frac{L}{2}$$
64. A fully charged capacitor $$C$$ with initial charge $${q_0}$$ is connected to a coil of self inductance $$L$$ at $$t = 0.$$ The time at which the energy is stored equally between the electric and the magnetic fields is:
A
$$\frac{\pi }{4}\sqrt {LC} $$
B
$$2\pi \sqrt {LC} $$
C
$$\sqrt {LC} $$
D
$$\pi \sqrt {LC} $$
Answer :
$$\frac{\pi }{4}\sqrt {LC} $$
65. Which of the following graphs represents the correct variation of capacitive reactance $${X_C}$$ with frequency $$\upsilon $$ ?
A
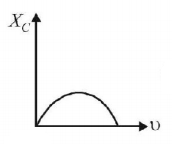

B
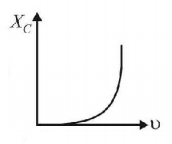

C
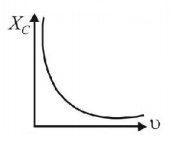

D
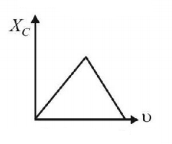

Answer :


66. The self inductance of the motor of an electric fan is $$10 H.$$ In order to impart maximum power at $$50 Hz,$$ it should be connected to a capacitance of
A
$$8\mu F$$
B
$$4\mu F$$
C
$$2\mu F$$
D
$$1\mu F$$
Answer :
$$1\mu F$$
67. If an $$LCR$$ series circuit is connected to an $$ac$$ source, then at resonance the
A
voltage across $$R$$ is zero
B
voltage across $$R$$ equals the applied voltage
C
voltage across $$C$$ is zero
D
voltage across $$L$$ equals the applied voltage
Answer :
voltage across $$R$$ equals the applied voltage
68.
In an experiment, $$200\,V\,AC$$ is applied at the ends of an $$LCR$$ circuit. The circuit consists of an inductive reactance
$$\left( {{X_L}} \right) = 50\,\Omega ,$$ capacitive reactance
$$\left( {{X_C}} \right) = 50\,\Omega $$ and ohmic resistance
$$\left( R \right) = 10\,\Omega .$$ The impedance of the circuit is
A
$$10\,\Omega $$
B
$$20\,\Omega $$
C
$$30\,\Omega $$
D
$$40\,\Omega $$
Answer :
$$10\,\Omega $$
69. The core of a transformer is laminated because
A
energy losses due to eddy currents may be minimised
B
the weight of the transformer may be reduced
C
rusting of the core may be prevented
D
ratio of voltage in primary and secondary may be increased
Answer :
energy losses due to eddy currents may be minimised
70. In an $$AC$$ circuit an alternating voltage $$e = 200\sqrt 2 \sin 100t\,volt$$ is connected to a capacitor of capacity $$1\,\mu F.$$ The $$rms$$ value of the current in the circuit is
A
$$100\,mA$$
B
$$200\,mA$$
C
$$20\,mA$$
D
$$10\,mA$$
Answer :
$$20\,mA$$