1.
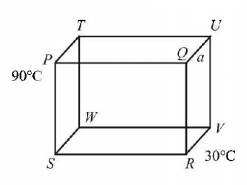
12 identical rods made of same material are arranged in the form of a cube. The temperature of $$P$$ and $$R$$ are maintained at $${90^ \circ }C$$ and $${30^ \circ }C$$ respectively. Then the temperature of point $$V,$$ when steady state is reached is
A
$${65^ \circ }C$$
B
$${60^ \circ }C$$
C
$${20^ \circ }C$$
D
$${50^ \circ }C$$
Answer :
$${50^ \circ }C$$
2. A mass of $$50g$$ of water in a closed vessel, with surroundings at a constant temperature takes $$2$$ minutes to cool from $${30^ \circ }C$$ to $${25^ \circ }C.$$ A mass of $$100g$$ of another liquid in an identical vessel with identical surroundings takes the same time to cool from $${30^ \circ }C$$ to $${25^ \circ }C.$$ The specific heat of the liquid is: (The water equivalent of the vessel is $$30g.$$ )
A
$$2.0\,kcal/kg$$
B
$$7\,kcal/kg$$
C
$$3\,kcal/kg$$
D
$$0.5\,kcal/kg$$
Answer :
$$0.5\,kcal/kg$$
3. A hammer of mass $$1\,kg$$ having speed of $$50\,m/s,$$ hit a iron nail of mass $$200\,gm.$$ If specific heat of iron is $$0.105\,cal/g{m^ \circ }C$$ and half the energy is converted into heat. the raise in temperature of nail is
A
$${7.1^ \circ }C$$
B
$${9.2^ \circ }C$$
C
$${10.5^ \circ }C$$
D
$${12.1^ \circ }C$$
Answer :
$${7.1^ \circ }C$$
4. Liquid oxygen at $$50\,K$$ is heated to $$300\,K$$ at constant pressure of $$1\,atm.$$ The rate of heating is constant. Which one of the following graphs represents the variation of temperature with time?
A
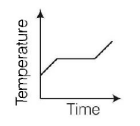

B
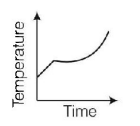

C
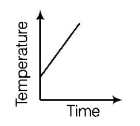

D
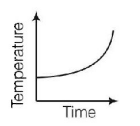

Answer :


5. If liquefied oxygen at 1 atmospheric pressure is heated from $$50\,k$$ to $$300\,k$$ by supplying heat at constant rate. The graph of temperature vs time will be
A
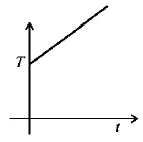

B
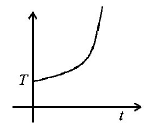

C
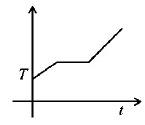

D
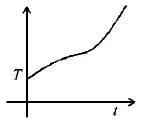

Answer :


6. A piece of ice falls from a height $$h$$ so that it melts completely. Only one-quarter of the heat produced is absorbed by the ice and all energy of ice gets converted into heat during its fall. The value of $$h$$ is [Latent heat of ice is $$3.4 \times {10^5}J/kg$$ and $$g = 10\,N/kg$$ ]
A
$$544\,km$$
B
$$136\,km$$
C
$$68\,km$$
D
$$34\,km$$
Answer :
$$136\,km$$
7. A block of ice at $$ - {10^ \circ }C$$ is slowly heated and converted to steam at $${100^ \circ }C.$$ Which of the following curves represents the phenomenon qualitatively
A
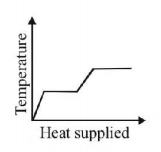

B
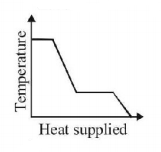

C
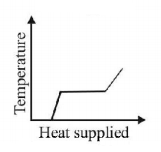

D
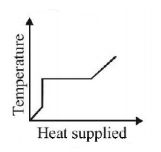

Answer :


8. Assuming no heat losses, the heat released by the condensation of $$xg$$ of steam at $${100^ \circ }C$$ can be used to convert $$yg$$ of ice at $${0^ \circ }C$$ into water at $${100^ \circ }C,$$ the ratio $$x:y$$ is:
A
$$1:1$$
B
$$1:2$$
C
$$1:3$$
D
$$3:1$$
Answer :
$$1:3$$
9. The room heater can maintain only $${16^ \circ }C$$ in the room when the temperature outside is $${-20^ \circ }C.$$ It is not warm and comfortable, that is why the electric stove with power of $$1kW$$ is also plugged in. Together these two devices maintain the room temperature of $${22^ \circ }C.$$ Determine the thermal power of the heater.
A
$$3kW$$
B
$$4kW$$
C
$$5kW$$
D
$$6kW$$
Answer :
$$6kW$$
10. In an energy recycling process, $$100\,g$$ of steam at $${100^ \circ }C$$ becomes water at $${100^ \circ }C$$ which converts $$yg$$ of ice at $${0^ \circ }C$$ into water at $${100^ \circ }C.$$ The numeric value of $$y$$ is
A
100
B
200
C
300
D
400
Answer :
300